LU分解のやり方と連立方程式を解くときのうれしさ

具体例

例えば、$A=\begin{pmatrix}1&2\\3&4\end{pmatrix}$ に対して、
$L=\begin{pmatrix}1&0\\3&1\end{pmatrix}$、$U=\begin{pmatrix}1&2\\0&-2\end{pmatrix}$
とすれば、$A=LU$ となります。

LU分解と連立方程式

LU分解を使って
$A\overrightarrow{x}=\overrightarrow{b}$
という連立方程式を解くことができます。

手順１．$A$ のLU分解を求める。
$A=LU$ なる $L$ と $U$ を求めます。求め方は後述します。

手順２．$LU\overrightarrow{x}=\overrightarrow{b}$ を解く。
$LU\overrightarrow{x}=\overrightarrow{b}$ という方程式は、
$U\overrightarrow{x}=\overrightarrow{y}$
とおくと、
$L\overrightarrow{y}=\overrightarrow{b}$
のように書き換えることができます。

そこで、まずは $L\overrightarrow{y}=\overrightarrow{b}$を使って $\overrightarrow{y}$ を求めてから、$U\overrightarrow{x}=\overrightarrow{y}$ を使って $\overrightarrow{x}$ を求めます。

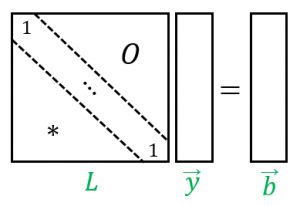
$\overrightarrow{y}$ を求める部分は、$L$ の右上半分が $0$ なので、$\overrightarrow{y}$ の先頭の成分から順々に計算できます。

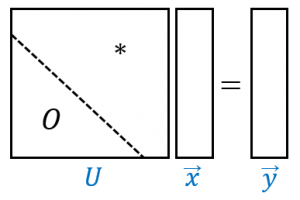
$\overrightarrow{x}$ を求める部分は、$U$ の左下半分が $0$ なので、$\overrightarrow{x}$ の後ろ成分から順々に計算できます。

LU分解による方法はうれしい？

手順１の計算量は $O(n^3)$ です。
手順２の計算量は $O(n^2)$ です。
よって、この方法で連立方程式を解くためにかかる計算量は $O(n^3)$ になります。

LU分解がうれしいのは、
$A\overrightarrow{x}=\overrightarrow{b}_1$
$A\overrightarrow{x}=\overrightarrow{b}_2$
$A\overrightarrow{x}=\overrightarrow{b}_3$
$\vdots$
のように、$A$ が共通で $\overrightarrow{b}$ が異なる連立方程式を複数解きたい場合です。

この場合、手順１（LU分解）は１回だけやればOKで、各方程式に対して手順２をやるだけでよいです。そのため、各連立方程式に対してガウスの消去法を使う場合よりは計算時間を節約できます。

LU分解の求め方

１．$A$ の一行目を見て、$U$ の一行目を計算する
２．$A$ の一列目を見て、$L$ の一列目を計算する
３．$A$ の二行目を見て、$U$ の二行目を計算する
４．$A$ の二列目を見て、$L$ の二列目を計算する
$\vdots$
という流れで計算することができます。

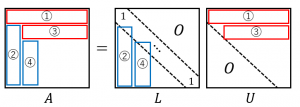
例えば、$3\times 3$ 行列の場合、
$\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}$
$=\begin{pmatrix}1&0&0\\l_{21}&1&0\\l_{31}&l_{32}&1\end{pmatrix}\begin{pmatrix}u_{11}&u_{12}&u_{13}\\0&u_{22}&u_{23}\\0&0&u_{33}\end{pmatrix}$
という分解は、以下のように計算できます。

１．$U$ の一行目を計算する
$a_{11}=u_{11}$
$a_{12}=u_{12}$
$a_{13}=u_{13}$
から $U$ の一行目が分かります。

２．$L$ の一列目を計算する
$a_{21}=l_{21}u_{11}$
$a_{31}=l_{31}u_{11}$
から $L$ の一列目が分かります（$u_{11}$ はすでに分かっていることに注意してください）。

３．$U$ の二行目を計算する
$a_{22}=l_{21}u_{12}+u_{22}$
$a_{23}=l_{21}u_{13}+u_{23}$
から $U$ の二行目が分かります。

以下、同様に、$L$ の二列目→$U$ の三行目を計算して終了です。

LU 分解と行列式

$A=LU$
のように $LU$ 分解できたら、$A$ の行列式は簡単に求めることができます。

実際、
$\det A=\det LU\\
=(\det L)(\det U)$
ですが、下三角行列と上三角行列の行列式は、対角成分の積なので簡単に求めることができます。

関連：行列式の公式、性質一覧

次回は 行列の積の計算方法と例題 を解説します。