Jaccard係数、Dice係数、Simpson係数

「集合 $X$ と集合 $Y$ がどれくらい似ているか」を表す３つの係数を紹介します。

Jaccard 係数

集合 $X$ と集合 $Y$ に対して $\dfrac{|X\cap Y|}{|X\cup Y|}$ のことをJaccard係数と言います。

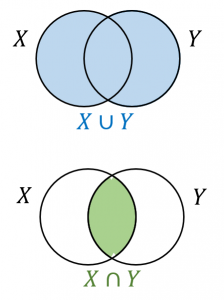
$X$ または $Y$ に含まれている要素のうち $X$ にも $Y$ にも含まれている要素の割合を表します。

例えば、$X=\{a,b,c\}$、$Y=\{a,b,d,e\}$ のとき、
$|X\cap Y|=2$、$|X\cup Y|=5$ なので、Jaccard係数は $\dfrac{2}{5}$ になります。

Jaccard係数が大きいほど（１に近いほど）$X$ と $Y$ は似ていると言えます。

Dice 係数

集合 $X$ と集合 $Y$ に対して $\dfrac{2|X\cap Y|}{|X|+|Y|}$ のことをDice係数と言います。

Jaccard係数の定義式の分母は $X$ にも $Y$ にも含まれている要素の数でしたが、これを「$X$ の要素数と $Y$ の要素数の平均」に変えるとDice係数になります。

例えば、$X=\{a,b,c\}$、$Y=\{a,b,d,e\}$ のとき、
$|X|=3$、$|Y|=4$、$|X\cap Y|=2$ なので、Dice係数は $\dfrac{2\times 2}{4+3}=\dfrac{4}{7}$ になります。

Dice係数が大きいほど（１に近いほど）$X$ と $Y$ は似ていると言えます。

Simpson 係数

集合 $X$ と集合 $Y$ に対して $\dfrac{|X\cap Y|}{\min(|X|,|Y|)}$ のことをSimpson係数と言います。

Jaccard係数の定義式の分母は $X$ にも $Y$ にも含まれている要素の数でしたが、これを「$X$ の要素数と $Y$ の要素数のうちの小さい方」に変えるとSimpson係数になります。

例えば、$X=\{a,b,c\}$、$Y=\{a,b,d,e\}$ のとき、
$|X|=3$、$|Y|=4$、$|X\cap Y|=2$ なので、Simpson係数は $\dfrac{2}{3}$ になります。

Simpson係数が大きいほど（１に近いほど）$X$ と $Y$ は似ていると言えます。

３つの係数の性質

共通の性質
・Jaccard係数、Dice係数、Simpson係数は、いずれも $0$ 以上 $1$ 以下です。
・$X$ と $Y$ が共通部分を持たないとき、３つの係数は全て $0$ になります。類似度は０と考えることができます。
・$X$ と $Y$ が一致するとき、３つの係数は全て $1$ になります。類似度は１と考えることができます。

異なる性質
・$X$ と $Y$ の片方が、もう片方の真部分集合のとき、Simpson係数は $1$ になりますが、Jaccard係数とDice係数は $1$ にはなりません。
（参考：→部分集合と真部分集合の違い）

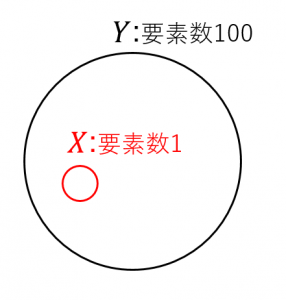
例えば、図のような場合、
Jaccard係数：$\dfrac{1}{100}$
Dice係数：$\dfrac{2}{101}$
Simpson係数：$1$
になります。
図のような２つの集合を「似ている」とみなしたいときにはSimpson係数を使うとよいでしょう。「似ていない」とみなしたいときにはJaccard係数またはDice係数を使うとよいでしょう。

・同じ $X$ と $Y$ に対しては、Simpson係数はDice係数以上です。
・同じ $X$ と $Y$ に対しては、Dice係数はJaccard係数以上です。

次回は 主成分分析が共分散行列の固有値問題に対応することの２通りの証明 を解説します。