放物線とカテナリー曲線の長さを計算する

曲線 $y=f(x)$ の $a\leq x\leq b$ の部分の長さは、
$\displaystyle\int_a^b\sqrt{1+(y’)^2}dx$
という定積分で計算できる。

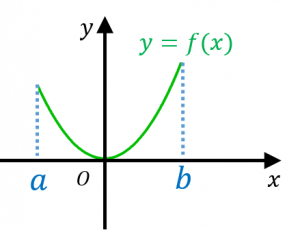
この公式を使って、放物線とカテナリー曲線の長さを計算してみましょう。

放物線の長さ

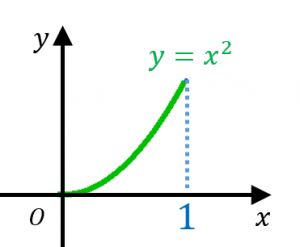
$y’=2x$ なので、公式を使うと、放物線の長さは、
$\displaystyle\int_0^1\sqrt{1+(2x)^2}\:dx\\
=\displaystyle\int_0^1\sqrt{4x^2+1}\:dx\\
=2\displaystyle\int_0^1\sqrt{x^2+\dfrac{1}{4}}\:dx$
となります。この積分計算は大変ですが、√x^2+1の積分を3ステップで解説で紹介した公式を使うと、上式は
$\left[x\sqrt{x^2+\dfrac{1}{4}}+\dfrac{1}{4}\log\left(\sqrt{x^2+\dfrac{1}{4}}+x\right)\right]_0^1\\
=\sqrt{\dfrac{5}{4}}+\dfrac{1}{4}\log\left(\sqrt{\dfrac{5}{4}}+1\right)-\dfrac{1}{4}\log\dfrac{1}{2}\\
=\dfrac{\sqrt{5}}{2}+\dfrac{1}{4}\log(2+\sqrt{5})\\
\fallingdotseq 1.4789$
となります。

$(0,0)$ と $(1,1)$ を結ぶ線分の長さが $\sqrt{2}\fallingdotseq 1.414$ なので、それより少し長いくらいです。

カテナリー曲線の長さ

$y’=\dfrac{1}{2}(e^{x}-e^{-x})$ なので、公式を使うと、カテナリー曲線の長さは、
$\displaystyle\int_0^1\sqrt{1+\dfrac{1}{4}(e^{x}-e^{-x})^2}\:dx\\
=\displaystyle\int_0^1\sqrt{\dfrac{1}{4}\{(e^{x})^2+2+(e^{-x})^2\}}\:dx\\
=\displaystyle\int_0^1\dfrac{1}{2}(e^{x}+e^{-x})dx\\
=\dfrac{1}{2}\left(e-\dfrac{1}{e}\right)$

余談

一般のカテナリー曲線 $y=\dfrac{c}{2}(e^{\frac{x}{c}}+e^{-\frac{x}{c}})$ の $a\leq x\leq b$ の部分の長さは、上記と同様に計算できて、
$\dfrac{1}{2}c(e^{\frac{b}{c}}-e^{-\frac{b}{c}})-\dfrac{1}{2}c(e^{\frac{a}{c}}-e^{-\frac{a}{c}})$
となります。

これは、$\sinh x=\dfrac{e^x+e^{-x}}{2}$ という関数を使うと、
$c\sinh\dfrac{b}{c}-c\sinh\dfrac{a}{c}$
と表すことができます。

次回は 立体角の意味と計算の例 を解説します。