ひし形の面積を求める方法と例題

ひし形の面積を計算してみる

例題１

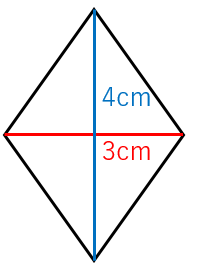
対角線の長さがそれぞれ $3\:\mathrm{cm}$ と $4\:\mathrm{cm}$ であるひし形の面積を計算せよ。

解答

公式より、ひし形の面積は、
$3\times 4\div 2=6\:\mathrm{cm}^2$

例題２

対角線の長さがそれぞれ $3.1\:\mathrm{cm}$ と $1.2\:\mathrm{cm}$ であるひし形の面積を計算せよ。

解答

対角線の長さが小数でもやることは同じです。公式より、ひし形の面積は、
$3.1\times 1.2\div 2\\
=3.1\times 0.6 =1.86\:\mathrm{cm}^2$

計算ツール

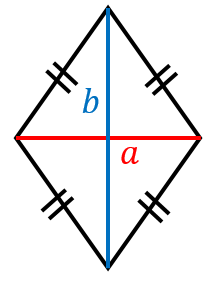
公式がなぜ成り立つか

ひし形の面積は、それを囲む長方形の面積の半分であることが分かります（図参照）。

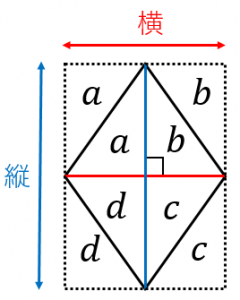
実際、
ひし形＝$a+b+c+d$
長方形＝$2a+2b+2c+2d$
だから、ひし形は長方形の半分！

そして、長方形の面積は、横の長さ×縦の長さ、すなわち、(ひし形の)対角線の長さ×(ひし形の)対角線の長さと等しくなります。

よって、ひし形の面積＝対角線の長さ×対角線の長さ÷2
となります。

関連：図形の面積を求める公式たち19個

辺の長さから面積を求める

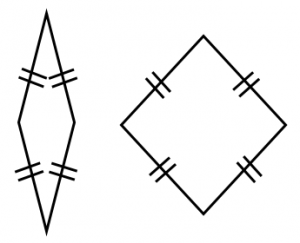
例えば、図のような2つのひし形を考えてみます。辺の長さは同じですが、面積は全く異なります（片方はつぶれていて面積が小さい、片方は正方形に近くて面積が大きい）。

一辺の長さだけでなく他の情報（角度など）が分かれば面積を求めることができます。

例題３

一辺の長さが $2$ で、一つの角度が $60^{\circ}$ であるひし形の面積を求めよ。

解答

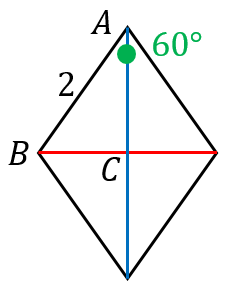
三角形 $ABC$ は $30^{\circ}$、$60^{\circ}$、$90^{\circ}$ の直角三角形なので、$BC=1$、$AC=\sqrt{3}$ となります（中学数学で習う知識）。

よって、対角線の長さは $2$ と $2\sqrt{3}$ です。よって、求める面積は、$2\times 2\sqrt{3}\div 2=2\sqrt{3}$

次回は 平行四辺形、ひし形、長方形、正方形の違い を解説します。