平行軸の定理を分かりやすく説明【慣性モーメントの計算】

ただし、
$I$ は任意の軸まわりの慣性モーメント
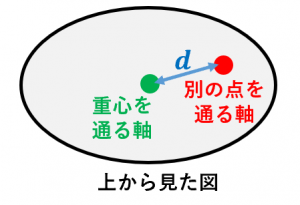
$I_G$ は（考えている軸と平行で）重心を通る軸まわりの慣性モーメント
$M$ は質量、$d$ は重心から軸までの距離です。

平行軸の定理を使った計算例

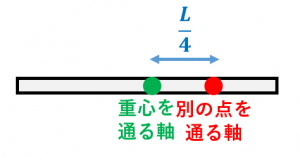
例えば、長さ $L$、質量 $M$ の一様な棒の、重心から $\dfrac{L}{4}$ の点を通る軸についての慣性モーメントを計算してみましょう。

一様な棒の、重心を通る軸まわりの慣性モーメントは、
$I_G=\dfrac{1}{12}ML^2$
です。
参考：一様な棒の慣性モーメントの計算方法と考察

よって、平行軸の定理を使うと、求める慣性モーメントは、
$I_G+Md^2\\
=\dfrac{1}{12}ML^2+M\left(\dfrac{L}{4}\right)^2\\
=\dfrac{1}{12}ML^2+\dfrac{1}{16}ML^2\\
=\dfrac{7}{48}ML^2$
のように計算できます。

平行軸の定理の証明

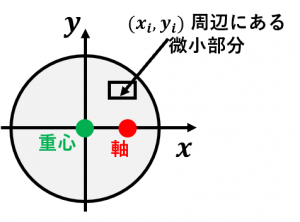
このとき、図形を微小部分に分割して、微小部分 $i$ から軸までの距離を $a_i$ とおくと、
$I=\displaystyle\sum_i m_ia_i^2$
となります。余弦定理を使うと、
$I=\displaystyle\sum_i m_i\{(x_i^2+y_i^2)+d^2-2dx_i\}$
となります。和を分解すると、第一項は $I_G$ となり、第二項は $Md^2$ になり、第三項は重心の定義より $\displaystyle\sum_{i}x_i=0$ なので、$0$ になります。

以上より、
$I=I_G+Mh^2$
となります。

平行軸の定理の応用方法

手順1. 重心まわりの慣性モーメント $I_G$ を計算する
手順2. 平行軸の定理を使って $I$ を計算する

そのため、いろいろな図形について、重心まわりの慣性モーメントを覚えておく（計算できるようになっておく）ことが重要です。

棒の慣性モーメント：
重心を通る軸まわりの慣性モーメントは、$\dfrac{1}{12}ML^2$

長方形や正方形の慣性モーメント：
重心を通る軸まわりの慣性モーメントは、$\dfrac{1}{3}M(a^2+b^2)$
ただし、横の長さを $2a$、縦の長さを $2b$ としました。
一様な長方形・正方形の慣性モーメントの２通りの計算

円盤の慣性モーメント：
重心を通る軸まわりの慣性モーメントは、$\dfrac{1}{2}Mr^2$
ただし、$r$ は円盤の半径です。

次回は 一様な円柱と円錐の慣性モーメント を解説します。