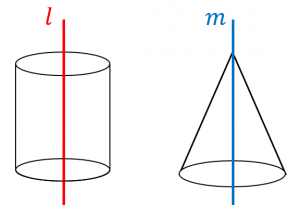
半径が $R$、質量が $M$ の一様な円柱について、回転軸 $l$ のまわりの慣性モーメントは、$I=\dfrac{1}{2}MR^2$
底面の半径が $R$、質量が $M$ の一様な円錐について、回転軸 $m$ のまわりの慣性モーメントは、$I=\dfrac{3}{10}MR^2$
円柱の慣性モーメント
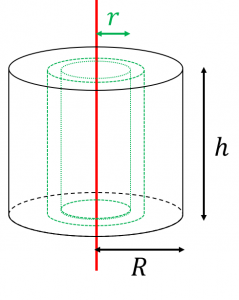
まず、大きな円柱の密度は、
$\rho = M\div \pi R^2h$ です。
また、円柱の高さを $h$ とすると、この微小部分の体積は、
$\Delta V=2\pi r\Delta r\times h$ とみなせます。
よって、微小部分の質量は、
$\begin{aligned}\Delta m&=\rho \Delta V\\&=\dfrac{M}{\pi R^2h}\cdot 2\pi rh\Delta r\\&=\dfrac{2Mr}{R^2}\Delta r\end{aligned}$
となります。
よって、
$\begin{aligned}\Delta I&=r^2\Delta m\\&=\dfrac{2M}{R^2}r^3\Delta r\end{aligned}$
となります。これを積分すると、
$\begin{aligned}I&=\displaystyle\int_0^R\dfrac{2M}{R^2}r^3 dr\\&=\dfrac{2M}{R^2}\cdot\dfrac{R^4}{4}\\&=\dfrac{1}{2}MR^2\end{aligned}$
となります。
薄い円板の慣性モーメント
円柱の慣性モーメントは、$\dfrac{1}{2}MR^2$ でした。これは、円柱の高さ $h$ には依存していません。
したがってどんなに薄い円板でも、慣性モーメントは $\dfrac{1}{2}MR^2$ になります。
円錐の慣性モーメント
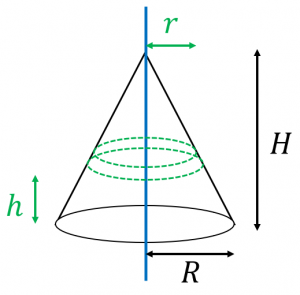
この微小部分は薄い円板とみなせるので、質量を $\Delta m$、半径を $r$ とすると、上記の薄い円板の慣性モーメントの結果から、
$\Delta I=\dfrac{1}{2}r^2\Delta m$
となります。
あとは、$r$ と $\Delta m$ をそれぞれ求めて積分すればOKです。
まず、円錐の高さを $H$ とすると、$r=R\times\dfrac{h}{H}$ となります。
次に、$\Delta m$ ですが、円錐の密度が
$\rho = M\div \dfrac{1}{3}\pi R^2H$
であることと、
この薄い円板の体積が
$\Delta V=\pi r^2\Delta h$
であることから、
微小部分の質量は、
$\begin{aligned}\Delta m&=\rho \Delta V\\&=\dfrac{3M\pi r^2}{\pi R^2H}\Delta h\\&=\dfrac{3Mr^2}{R^2H}\Delta h\end{aligned}$
となります。
以上により、
$\begin{aligned}\Delta I&=\dfrac{1}{2}r^2\Delta m\\&=\dfrac{1}{2}\cdot\dfrac{3M}{R^2H}r^4\Delta h\end{aligned}$
となります。これを積分すると、
$\begin{aligned}I&=\displaystyle\int_0^H\dfrac{1}{2}\cdot\dfrac{3M}{R^2H}r^4 dh\\&=\displaystyle\int_0^H\dfrac{3M}{2R^2}\cdot\dfrac{R^4h^4}{H^5}dh\\&=\dfrac{3MR^2}{2}\cdot\dfrac{1}{H^5}\cdot\dfrac{1}{5}H^5\\&=\dfrac{3}{10}MR^2\end{aligned}$
となります。
次回は アルコールの度数や量を計算する公式といろいろな例 を解説します。
