一様な棒の慣性モーメントの計算方法と考察

※「重心まわり」とは「重心を通り棒に垂直な軸に関する」の意味です。

重心まわりの慣性モーメント

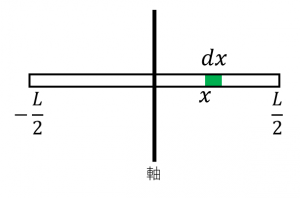
重心からの距離が $x$ から $x+dx$ の間にある部分の質量は $M\cdot\dfrac{dx}{L}$ なので、
$\begin{aligned}I&=\displaystyle\int_{-\frac{L}{2}}^{\frac{L}{2}}x^2\cdot \dfrac{Mdx}{L}\\&=\dfrac{M}{L}\displaystyle\int_{-\frac{L}{2}}^{\frac{L}{2}}x^2dx\\&=\dfrac{M}{L}\cdot\dfrac{L^3}{12}\\&=\dfrac{1}{12}ML^2\end{aligned}$

端点まわりの慣性モーメント

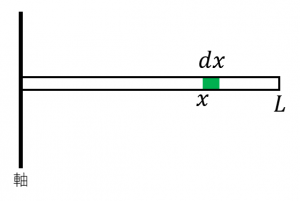
端点からの距離が $x$ から $x+dx$ の間にある部分の質量は $M\cdot\dfrac{dx}{L}$ なので、
$\begin{aligned}I&=\displaystyle\int_{0}^{L}x^2\cdot \dfrac{Mdx}{L}\\&=\dfrac{M}{L}\displaystyle\int_{0}^{L}x^2dx\\&=\dfrac{M}{L}\cdot\dfrac{L^3}{3}\\&=\dfrac{1}{3}ML^2\end{aligned}$

平行軸の定理

慣性モーメントに関する平行軸の定理：
$I=I_G+Mh^2$
を確認してみましょう。

$I_G$：重心まわりの慣性モーメント、$\dfrac{1}{12}ML^2$
$h$：重心と端点の距離、$\dfrac{L}{2}$

とすると、
$\begin{aligned}&I_G+Mh^2\\&=\dfrac{1}{12}ML^2+M\cdot\left(\dfrac{L}{2}\right)^2\\&=\dfrac{1}{12}ML^2+\dfrac{1}{4}ML^2\\&=\dfrac{1}{3}ML^2\end{aligned}$
となり、さきほど計算した $I$ と一致しています。確かに平行軸の定理が成立しています。

平行軸の定理を覚えていれば、$I$ と $I_G$ のうち片方を忘れても、もう片方から計算することができます。

棒を分割する

長さ $L$ で質量 $M$ の棒は、
長さ $\dfrac{L}{2}$ で質量 $\dfrac{M}{2}$ の棒２本とみなすことができます。

よって、
「長さ $L$ で質量 $M$ の棒の重心まわりの慣性モーメント」は、
「長さ $\dfrac{L}{2}$ で質量 $\dfrac{M}{2}$ の棒の端点まわりの慣性モーメント」の２倍になります。

これを使うと、
$I=\dfrac{1}{3}ML^2$
から、
$\begin{aligned}I_G&=\dfrac{1}{3}\left(\dfrac{M}{2}\right)\left(\dfrac{L}{2}\right)^2\times 2\\&=\dfrac{1}{12}ML^2\end{aligned}$
というように、$I_G$ を計算することができます。

次回は 一様な長方形・正方形の慣性モーメントの２通りの計算 を解説します。