行列の内積の定義と性質

通常の行列の積について確認してから、行列の内積について解説します。

行列の積

「通常の」行列の積は、図のようにベクトルの内積を使って定義されます。

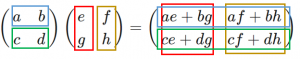
詳しくは 行列の積の計算方法と例題 を参照してください。

この記事では、行列同士の別の種類のかけ算である、行列の内積（Frobenius Product）について紹介します。

行列の内積の定義

例えば、
$A=\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}$、$B=\begin{pmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{pmatrix}$
のとき、
$A\cdot B=a_{11}b_{11}+a_{12}b_{12}+a_{21}b_{21}+a_{22}b_{22}$
です。

このように定義した $A\cdot B$ は、内積が満たすべき性質を満たします。つまり、$A\cdot B$ は行列の内積となります。

行列の内積と順番

まず、定義より、$A\cdot B=B\cdot A$ であることが分かります。順番を交換しても値は同じです。

行列の内積とトレース

※$\mathrm{tr}(A)$ は $A$ の対角成分の和：
$\displaystyle\sum_{i=1}^na_{ii}$
のことです。

これを証明してみましょう。
まず、$A^{\top}$ の $k$ 行目は（$A$ を転置していることに注意すると）、
$\begin{pmatrix}a_{1k}&a_{2k}&\cdots &a_{nk}\end{pmatrix}$
で、$B$ の $k$ 列目は、
$\begin{pmatrix}b_{1k}\\b_{2k}\\\vdots\\b_{nk}\end{pmatrix}$
なので、$A^{\top}B$ の $kk$ 成分は、
$c_k=\displaystyle\sum_{i=1}^na_{ik}b_{ik}$
となります。

・$\mathrm{tr}(A^{\top}B)$ は、$c_k$ を $k=1$ から $k=n$ まで足し上げたものです。
・そして、実際に $\displaystyle\sum_{k=1}^nc_k$ について考えると、これは、$A$ と $B$ の対応する成分の積の全ての和、つまり、$A\cdot B$ になっています。

次回は 線形代数の意味、何の役に立つか、などを紹介 を解説します。