弧の長さ、弦の長さに関する性質を整理しました。
弧の長さ
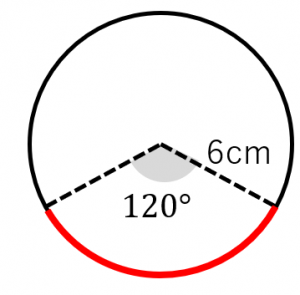
円周の長さは
$2\pi\times 6=12\pi\:\mathrm{cm}$
なので、扇形の弧の長さは、
$12\pi\times\dfrac{120}{360}\\
=4\pi\:\mathrm{cm}$
となります。
一般に、半径が $r$ で中心角が $\alpha^{\circ}$ である扇形の弧の長さは、
$2\pi r\times\dfrac{\alpha}{360}=\dfrac{\pi r\alpha}{180}$
となります。
弧度法の場合(つまり、中心角が $\theta$ ラジアンの場合)弧の長さは
$r\theta$
となります。
弦の長さ
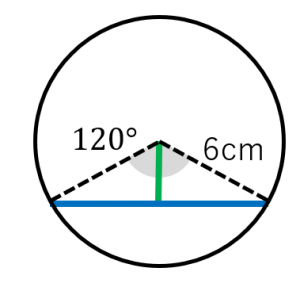
弦は、二等辺三角形の底辺になります。垂直二等分線を引くと、$30^{\circ},60^{\circ},90^{\circ}$ の直角三角形が2つ現れます。弦の長さは、
$6\times\dfrac{\sqrt{3}}{2}\times 2=6\sqrt{3}\:\mathrm{cm}$
となります。
一般に、半径が $r$ で中心角が $\theta$ である場合の弦の長さは、
$2r\sin\dfrac{\theta}{2}$
となります。
弧の長さ、弦の長さと円周角
弧の長さは、$r\theta$ と表されました。これは、$\theta$ が増えると大きくなります。
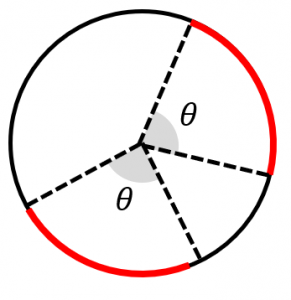
よって、同じ円について弧の長さが等しいなら中心角 $\theta$ が等しいことが分かります。
さらに、円周角は中心角の半分なので、弧の長さが等しいなら対応する円周角の大きさも等しいと言えます。
同様に、弦の長さが等しいなら対応する円周角の大きさが等しいことも証明できます。
比較
弧の長さは、$r\theta$ と表されるので、中心角に比例します。一方、弦の長さは、$2r\sin\dfrac{\theta}{2}$ と表されるので、中心角には比例しません。
また、中心角が等しい場合、弧の長さは弦の長さよりも長いです。
どちらも、$0^{\circ}\leq \theta\leq 180^{\circ}$ の範囲では狭義単調増加です。つまり、この範囲では、弧の長さが長いほど弦の長さも長いと言えます。
次回は 三角形の面積を3辺の長さから求める2つの方法 を解説します。
