三角形の面積を３辺の長さから求める２つの方法

三角形の３辺の長さが与えられたときに、面積を求める方法を２つ解説します。

１．sin の公式を使う方法

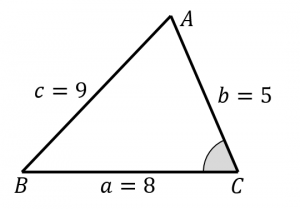
まず、余弦定理を使って、$\cos C$ を求めます：
$\cos C=\dfrac{5^2+8^2-9^2}{2\cdot 5\cdot 8}\\
=\dfrac{8}{80}\\
=\dfrac{1}{10}$

次に、$\sin^2C+\cos^2C=1$ を使って、$\sin C$ を求めます：
$\sin C=\sqrt{1-\cos^2C}\\
=\sqrt{1-\dfrac{1}{100}}\\
=\dfrac{3}{10}\sqrt{11}$

最後に、面積公式を使って、三角形の面積 $S$ を求めます：
$S=\dfrac{1}{2}ab\sin C\\
=\dfrac{1}{2}\cdot 8\cdot 5\cdot\dfrac{3}{10}\sqrt{11}\\
=6\sqrt{11}$

２．ヘロンの公式

先ほどの三角形の面積を求めてみます。
$a=8$、$b=5$、$c=9$ としてヘロンの公式を使うと、
$s=\dfrac{8+5+9}{2}=11$
$S=\sqrt{11(11-8)(11-5)(11-9)}\\
=\sqrt{11\cdot 3\cdot 6\cdot 2}\\
=6\sqrt{11}$

２つの方法の比較

sin の公式を使う方法のよい所
・解き方として分かりやすいので、記述式の試験などで使いやすい
・三辺の長さにルートなどが入っていても使える

ヘロンの公式のよい所
・計算がとても楽
・公式自体がきれいなので、気持ちがよい

ヘロンの公式の応用例

$s=\dfrac{a+a+a}{2}=\dfrac{3}{2}a$
なので、面積は、
$S=\sqrt{\dfrac{3}{2}a\left(\dfrac{1}{2}a\right)\left(\dfrac{1}{2}a\right)\left(\dfrac{1}{2}a\right)}\\
=\dfrac{\sqrt{3}}{4}a$
となります。

次回は 正三角形の面積の求め方（小学生用～高校生用） を解説します。