$r=l\times\dfrac{x}{360}$
という式を使うことで、
母線の長さ $l$、底面の半径 $r$、側面のおうぎ形の中心角 $x$ のうち2つが分かれば残りの1つを計算できる。

なお、
$r=l\times\dfrac{x}{360}$
がなせ成立するのかは円錐の側面積、底面積、表面積の求め方の後半「公式の証明」で解説しています。
母線の長さを求める
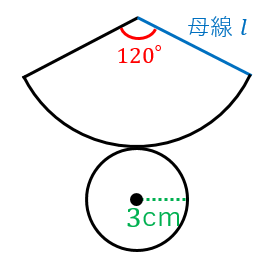
例題1:展開図が図のようになる円錐について、母線の長さを求めよ。
(側面のおうぎ形の中心角が $120^{\circ}$、底面の半径が $3\:\mathrm{cm}$)
$r=l\times\dfrac{x}{360}$
という公式で、$r=3$、$x=120$ とすると、
$3=l\times\dfrac{120}{360}$
となります。よって、母線の長さは、
$l=3\times\dfrac{360}{120}\\
=9\:\mathrm{cm}$
となります。
底面の半径を求める
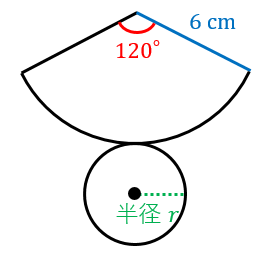
例題2:展開図が図のようになる円錐について、底面の半径の長さを求めよ。
(側面のおうぎ形の中心角が $120^{\circ}$、母線の長さが $6\:\mathrm{cm}$)
$r=l\times\dfrac{x}{360}$
という公式で、$l=6$、$x=120$ とすると、
$r=6\times\dfrac{120}{360}$
となります。よって、底面の半径の長さは、
$r=2\:\mathrm{cm}$
となります。
おうぎ方の中心角を求める
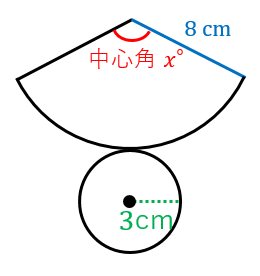
例題3:展開図が図のようになる円錐について、おうぎ方の中心角を求めよ。
(底面の半径が $3\:\mathrm{cm}$、母線の長さが $8\:\mathrm{cm}$)
$r=l\times\dfrac{x}{360}$
という公式で、$r=3$、$l=8$ とすると、
$3=8\times\dfrac{x}{360}$
となります。よって、中心角は、
$x=360\times\dfrac{3}{8}\\
=135^{\circ}$
となります。
まとめ
$r=l\times\dfrac{x}{360}$
という公式さえ覚えておけば、上記のような3つのタイプの問題は全て解くことができます。
次回は 半球の体積と表面積を計算する を解説します。
