半径 $R$ の半球の体積は、$\dfrac{2}{3}\pi R^3$
半径 $R$ の半球の表面積は、$3\pi R^2$
半球の体積

半径が $R$ の球の体積は $\dfrac{4}{3}\pi R^3$ です。
半球の体積は、球の体積の半分なので、$\dfrac{4}{3}\pi R^3\div 2=\dfrac{2}{3}\pi R^3$ になります。
例題1:半径が $3\:\mathrm{cm}$ の半球の体積を計算してみましょう。
公式を使うと、
$\dfrac{2}{3}\times\pi\times 3\times 3\times 3=18\pi\:\mathrm{cm}^3$
と計算できます。
円周率 $\pi$ はおおよそ $3.14$ なので、半球の体積はおおよそ、
$18\times 3.14=56.52\:\mathrm{cm}^3$
となります。
半球の表面積
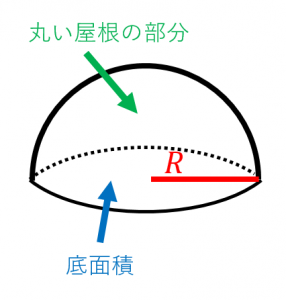
半球の表面積は、底面積+丸い屋根の部分です。
底面積は、半径 $R$ の円の面積なので、$\pi R^2$ です。
丸い屋根の部分は、半径が $R$ の球の表面積の半分なので、$4\pi R^2\div 2=2\pi R^2$ です。
(半径 $R$ の球の表面積が $4\pi R^2$ であることを使いました)
よって、半球の表面積は、$2\pi R^2+\pi R^2=3\pi R^2$ となります。
例題2:半径が $2\:\mathrm{cm}$ の半球の表面積を計算してみましょう。
公式を使うと、
$3\times\pi\times 2\times 2=12\pi\:\mathrm{cm}^2$
と計算できます。
円周率 $\pi$ はおおよそ $3.14$ なので、半球の体積はおおよそ、
$12\times 3.14=37.68\:\mathrm{cm}^3$
となります。
計算ツール

次回は 円錐台の体積と表面積を計算する公式と証明 を解説します。
