円周の長さの求め方と例題

円周の求め方：
(円周の長さ)＝(直径)×(円周率)

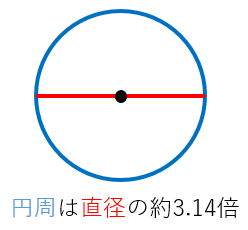
大雑把な値を計算したいときは、
(円周率) $=3.14$
とします。

例題

半径が $6$ ということは、直径はその $2$ 倍なので $12$ になります。

よって、円周率を $3.14$ とすると、
円周の長さは、
(直径)×$3.14$
なので、
$12\times 3.14=37.68$
となります。

円周率を3で習った方は、
$12\times 3=36$
が答えになります。

中学数学以降では、円周率を $\pi$ とすることが多いです。その場合、
円周の長さは、
$12\times \pi$
となります。

円周率がなぜ3.14くらいなのか

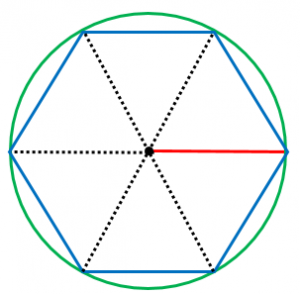
円の内側に接する正六角形を書いてみます。正六角形の周の長さは、半径6コぶんです。つまり、直径3コぶんです。

そして、円周の長さは正六角形の周の長さより少し長いくらいなので、
(円周の長さ)＝(直径)×(3+少し)
であることが分かります。

この (3+少し) の部分が円周率です。

円周率とは何なのか

(円周の長さ)＝(直径)×(円周率)
という公式について説明してきました。

実は、この式は公式というよりも、円周率の定義式です。円周率は
$\pi=3.14159265358979\cdots$
といつまでも続く数（無限小数）であることが知られています（途中で終わらないことの証明は難しいです）。

円周率を（分母と分子が整数であるような）分数で表すことはできません（無理数と呼ばれる数です）。→有理数と無理数の意味といろいろな例

次回は おうぎ形の弧長、面積、中心角、半径 を解説します。