指数関数 $y=e^x$ のグラフの概形を書くときに注意すべきコツを6個解説します。
$y=e^x$ のグラフ
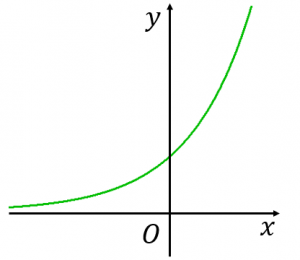
$y=e^x$ のグラフの概形は図のようになります。グラフを書くときには以下のポイントに気をつけましょう。
ポイント1:
値域は $y > 0$
$x$ がどんな値のときも、$e^x$ は $0$ より大きいです。そのため、グラフは $x$ 軸よりも上側にあります。
ポイント2:
単調増加
$x$ の値が増えれば増えるほど $y$ の値は増加します。これは、微分が $(e^x)’=e^x > 0$ であることからも分かります。
ポイント3:
右側では $x$ が増えると $y$ が急激に増える
$e^x$ は単調増加ですが、増え方は右に行くほど激しくなります。これは、導関数 $e^x$ が単調増加であることから分かります。「指数関数 $e^x$ は $x$ を増やすと爆発的に増える」という事実は覚えておきましょう。
関連:極限の基本的な公式、考え方一覧
漸近線
ポイント4:
$x$ 軸が漸近線
$x$ がどんどん小さくなると、$e^x$ はどんどん $0$ に近づきます。数式で書くと、$\displaystyle\lim_{x\to -\infty}e^x=0$ となります。
つまり、左側の方では $y=e^x$ のグラフは $x$ 軸に近づきます。
ちなみに、漸近線は $x$ 軸のみです。$y=e^x$ の右側($x\to\infty$)で漸近するような漸近線はありません。
$y$ 軸との交点、接線の傾き
ポイント5:
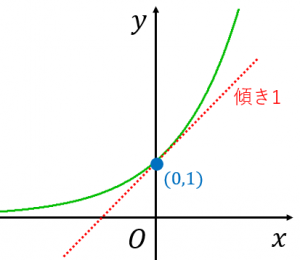
$(0,1)$ を通る
$x=0$ のとき、$e^x=1$ となります。つまり、$y=e^x$ のグラフは、$y$ 軸と $(0,1)$ で交わることになります。
ポイント6:
$x=0$ における接線の傾きは $1$
$y=e^x$ を微分すると、$e^x$ です。よって、$x=0$ における微分係数は $1$ となります。つまり、$x=0$ における接線の傾きは $1$ であることが分かります。接線と $y$ 軸のなす角が $45^{\circ}$ になるように意識しましょう。この接線は $(-1,0)$ も通ります。
ちなみに、$y=e^x$ のグラフを $y=x$ に関して折り返すと $y=\log x$ のグラフになります:
次回は y=logxのグラフの書き方:6つのポイント を解説します。
