横長の楕円
は横長の楕円を表します。
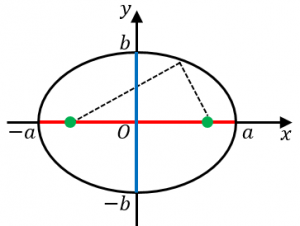
以下の5つの公式をセットで覚えておくとよいでしょう。
・$(a,0),(-a,0),(0,b),(0,-b)$ を通る
・長軸の長さ:$2a$
・短軸の長さ:$2b$
・焦点の座標:$(-\sqrt{a^2-b^2},0)$ と $(\sqrt{a^2-b^2},0)$
・楕円上の点は、焦点からの距離の和が $2a$ で一定
例題:$\dfrac{x^2}{9}+\dfrac{y^2}{4}=1$ という楕円について、長軸の長さ、短軸の長さ、焦点の座標、楕円上の点から焦点までの距離の和を求めてみましょう。
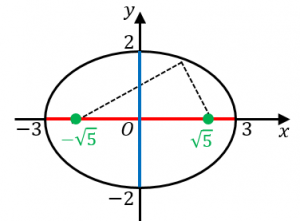
$a^2=9$、$b^2=4$ なので、$a=3$、$b=2$ として公式を使うと、
・長軸の長さは $6$
・短軸の長さは $4$
・$\sqrt{a^2-b^2}=\sqrt{9-4}=\sqrt{5}$ なので、
焦点の座標は、$(-\sqrt{5},0)$ と $(\sqrt{5},0)$
・楕円上の点は、焦点からの距離の和が $6$ で一定
となります。
縦長の楕円
は縦長の楕円を表します。
同じ式でも、$a$ が大きいか $b$ が大きいかによって、楕円が縦長か横長かが決まります。$a=b$ の場合は円になります。
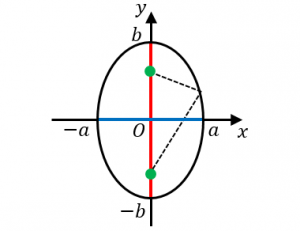
縦長の場合は以下の5つの公式が成立します。
・$(a,0),(-a,0),(0,b),(0,-b)$ を通る
・長軸の長さ:$2b$
・短軸の長さ:$2a$
・焦点の座標:$(0,-\sqrt{b^2-a^2})$ と $(0,\sqrt{b^2-a^2})$
・楕円上の点は、焦点からの距離の和が $2b$ で一定
その他の公式
$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$
という楕円(縦長の場合でも横長の場合でも)について、
・面積は $\pi ab$
・円の場合と違い、周の長さは簡単には計算できない
ことが知られています。また、楕円上の点 $(x_0,y_0)$ における接線の方程式は、
$\dfrac{x_0x}{a^2}+\dfrac{y_0y}{b^2}=1$
となります。
さらに、極座標における楕円の一般形は、
$r=\dfrac{l}{1+e\cos\theta}$
となります(ただし、$0 < e\leq 1$ で $e$ は離心率と呼ばれます)。
次回は 双曲線に関する公式まとめ を解説します。
