$\displaystyle\int\dfrac{1}{\tan^2x}dx=-\dfrac{1}{\tan x}-x+C$
計算方法1
$\displaystyle\int\dfrac{1}{\tan^2x}dx\\
=\displaystyle\int\dfrac{\cos^2x}{\sin^2x}dx\\
=\displaystyle\int\dfrac{1-\sin^2x}{\sin^2x}dx\\
=\displaystyle\int\left(\dfrac{1}{\sin^2x}-1\right)dx\\
=\displaystyle\int\dfrac{1}{\sin^2x}dx-\displaystyle\int 1dx\\
=-\dfrac{1}{\tan x}-x+C$
ただし、最後の変形で、
$\displaystyle\int\dfrac{1}{\sin^2x}dx=-\dfrac{1}{\tan x}+C$
であることを使いました。この積分公式については、
1/sin^2x と 1/cos^2x の積分と有名なテクニック
を参照してください。
計算方法2
$\displaystyle\int\dfrac{1}{\tan^2x}dx$
で、$\tan x=t$ と置換すると、
$\dfrac{dt}{dx}=\dfrac{1}{\cos^2x}=1+t^2$
なので、
$\displaystyle\int\dfrac{1}{t^2}\cdot\dfrac{dt}{1+t^2}$
となります。これを部分分数分解すると、
$\displaystyle\int\left(\dfrac{1}{t^2}-\dfrac{1}{1+t^2}\right)dt\\
=-\dfrac{1}{t}-\displaystyle\int\dfrac{1}{1+t^2}dt\\
=-\dfrac{1}{\tan x}-\displaystyle\int\dfrac{1}{1+t^2}dt$
となります。
この第二項の積分は、有名な積分公式を使うと、
$\displaystyle\int\dfrac{1}{1+t^2}dt=\mathrm{arctan}\:t=x$ となります。
(→arctanの意味、微分、不定積分)
結局、
$\displaystyle\int\dfrac{1}{\tan^2x}dx=-\dfrac{1}{\tan x}-x+C$
となります。
おまけ:グラフ
$y=\dfrac{1}{\tan^2x}$
($y=\cot^2x$)のグラフを書いてみました。
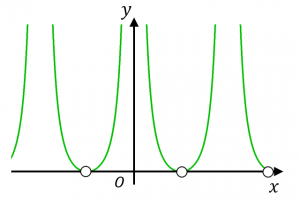
・左右対称です。
・定義域は、$\dfrac{\pi}{2}$ の整数倍以外の実数全体です。
・値域は、$y>0$ です。
次回は xe^{-x}の不定積分と広義積分 を解説します。
