円に内接する四角形の面積を求める公式

この公式のことを、ブラーマグプタの公式と言います。円に内接する四角形の面積を計算する公式について、例題と証明を解説します。

四角形の面積を計算する例題

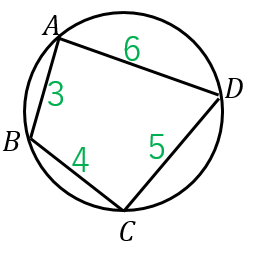
円に内接する四角形の面積公式：
$\sqrt{(s-a)(s-b)(s-c)(s-d)}$
$s=\dfrac{a+b+c+d}{2}$
を使ってみましょう。

まず、$s$ を計算します：
$s=\dfrac{3+4+5+6}{2}=\dfrac{18}{2}=9$

よって、面積は、
$\sqrt{(9-3)(9-4)(9-5)(9-6)}\\
=\sqrt{6\cdot 6\cdot 5\cdot 2}\\
=\sqrt{6\cdot 5\cdot 4\cdot 3}$
$=6\sqrt{10}$

簡単な計算で面積を求めることができました！

円に内接する四角形の面積公式の証明

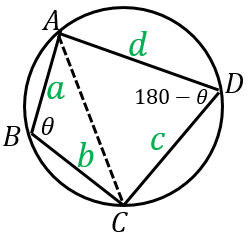
四角形の面積 $S$ は、
$\dfrac{1}{2}ab\sin\theta+\dfrac{1}{2}cd\sin(180^{\circ}-\theta)$
となります。ただし「円に内接する四角形の向かい合う角の和が $180^{\circ}$」であることを使いました。

よって、$\sin\theta=\sin(180^{\circ}-\theta)$ に注意すると面積の二乗は、
$S^2=\dfrac{1}{4}(ab+cd)^2\sin^2\theta\\
=\dfrac{1}{4}(ab+cd)^2(1-\cos^2\theta)$

となります。次に $\cos\theta$ を求めます。余弦定理を用いて対角線 $AC$ の長さを2通りの方法で表すと、
$a^2+b^2-2ab\cos\theta$
$=c^2+d^2-2cd\cos(180^{\circ}-\theta)$
となります。これを $\cos\theta$ について解くと、
$\cos\theta=\dfrac{a^2+b^2-c^2-d^2}{2(ab+cd)}$
となります。つまり、
$1-\cos^2\theta$
$=\dfrac{4(ab+cd)^2-(a^2+b^2-c^2-d^2)^2}{4(ab+cd)^2}$
となります。これを先ほどの式に代入すると、

$S^2=\dfrac{4(ab+cd)^2-(a^2+b^2-c^2-d^2)^2}{16}$

となります。この式の分子は、$A^2-B^2$ の形なので、
$(2ab+2cd+a^2+b^2-c^2-d^2)$
$\times(2ab+2cd-a^2-b^2+c^2+d^2)$
と因数分解できます。これはさらに以下のように因数分解できます：
$\{(a+b)^2-(c-d)^2\}$
$\times\{(c+d)^2-(a-b)^2\}$
$=(a+b+c-d)(a+b-c+d)$
$\times(a-b+c+d)(-a+b+c+d)$

これを $s$ を使って表すと、
$(2s-2d)(2s-2c)(2s-2b)(2s-2a)\\
=16(s-a)(s-b)(s-c)(s-d)$
となり、

$S^2=$$(s-a)(s-b)(s-c)(s-d)$
が分かりました。ブラーマグプタの公式が証明できました！

注意点

ブラーマグプタの公式は、4つの辺の長さから四角形の面積を計算する公式ですが、四角形が円に内接する場合のみ使えることに注意してください。

一般には、4つの辺の長さだけから面積を計算することはできません（4つの辺の長さを決めても四角形は1つには決まらない）。

関連：図形の面積を求める公式たち19個

次回は 正八面体の体積、表面積、外接球の半径、内接球の半径 を解説します。