漸近線の求め方３パターン

漸近線の「漸」には「しだいに」という意味があります。この記事では，高校数学で問われる漸近線の求め方３パターンについてそれぞれ解説します。

漸近線とは

漸近線とは「しだいに近づいていく直線」のことです。

「しだいに近づいていく」をもう少しきちんと言うと「十分遠くで距離が限りなく $0$ に近づいていく」です。この説明でだけでは漸近線の意味が分かりにくいので、3つの具体的な漸近線のパターンを解説します。

$y$ 軸に平行な漸近線

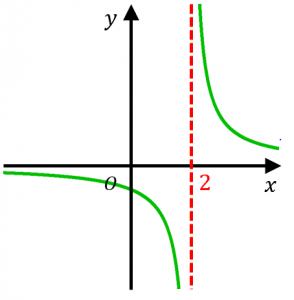
例えば、$y=\dfrac{1}{x-2}$ という分数関数について、
分母が $0$ になるのは $x=2$ です。実際、$x=2$ が漸近線になっています。

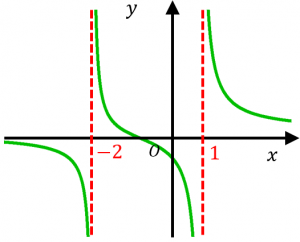
また、$y=\dfrac{x+1}{(x-1)(x+2)}$ という分数関数について、
分母が $0$ になるのは $x=1$ と $x=-2$ です。実際、$x=1$ と $x=-2$ が漸近線になっています。

一般に、
$\displaystyle\lim_{x\to a+0} f(x)=\infty$
$\displaystyle\lim_{x\to a+0} f(x)=-\infty$
$\displaystyle\lim_{x\to a-0} f(x)=\infty$
$\displaystyle\lim_{x\to a-0} f(x)=-\infty$
のどれか１つでも成り立てば、$x=a$ が漸近線になります。

分数関数のその他の漸近線

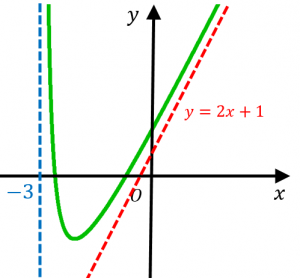
例えば、$f(x)=\dfrac{1}{x+3}+2x+1$ という分数関数では、
先ほど述べたことから分かるように（分母が $0$ になる点が $x=-3$ なので）$x=-3$ が漸近線ですが、それだけでなく、
$\displaystyle\lim_{x\to\infty}\{f(x)-(2x+1)\}=0$
となるので、$y=2x+1$ も漸近線になります。

一般には、$f(x)=\dfrac{2x^2+7x+4}{x+3}$ の漸近線を求めよ、というような形の問題が多いです。この場合は、わり算を実行して、
$f(x)=\dfrac{1}{x+3}+2x+1$
と変形することで、上記の問題と同じ形になります。結局、$y=2x+1$ が漸近線になることが分かります。

双曲線の漸近線

例えば、$\dfrac{x^2}{9}-\dfrac{y^2}{3}=1$ の漸近線は、$a=3$、$b=\sqrt{2}$ として公式を使うと、
$y=\dfrac{\sqrt{2}}{3}x$ と $y=-\dfrac{\sqrt{2}}{3}x$
となることが分かります。

関連：双曲線に関する公式まとめ

次回は 微分の公式全59個を重要度つきで整理 を解説します。