二等辺三角形の角度を計算する方法と例題を解説します。角度を計算するツールもご活用ください。
頂角から底角を求める
例題1:
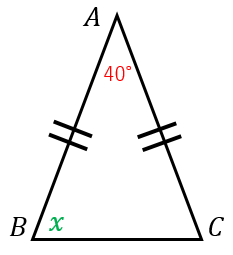
図のように、頂角が $40^{\circ}$ である二等辺三角形について、角度 $x$ を求めよ。
二等辺三角形の2つの底角は等しいです(→二等辺三角形の底角が等しいことの証明など)。
よって、$\angle C$ の大きさも $x$ です。
一方、三角形の内角の和は $180^{\circ}$ なので、
$\angle B+\angle C=180^{\circ}-40^{\circ}=140^{\circ}$
です。
$x$ が2つ分で $140^{\circ}$ なので、$x=70^{\circ}$ と分かります。
このように、頂角が分かっているときは、
180°から頂角の大きさを引いて2で割れば
底角の大きさが求まります。
底角から頂角を求める

例題2:
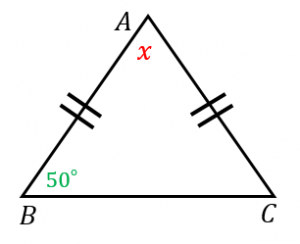
図のように、底角が $50^{\circ}$ である二等辺三角形について、角度 $x$ を求めよ。
二等辺三角形の2つの底角は等しいです。
よって、$\angle C$ の大きさも $50^{\circ}$ です。
よって、$\angle B +\angle C=100^{\circ}$ です。
三角形の内角の和は $180^{\circ}$ なので、$\angle A$ の大きさは、
$180^{\circ}-100^{\circ}=80^{\circ}$ となります。
このように、底角が分かっているときは、
180°から底角の2倍を引けば
頂角の大きさが求まります。
まとめ
・二等辺三角形では、3つの角度のうち1つが分かれば残りの角度も計算できます。
・計算には、
頂角+底角+底角=180°
という関係を使います。
・(おまけ)
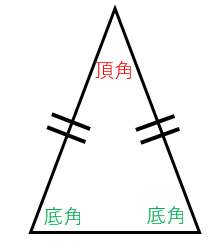
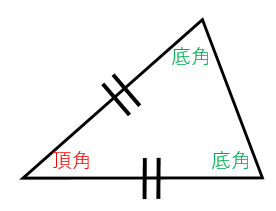
下の図のように二等辺三角形の向きが変わっても、頂角と底角を間違えないようにしましょう。等しい辺の間の角が頂角です。
次回は 対頂角、同位角、錯角の意味を分かりやすく解説 を解説します。
