交差確認（交差検証、Cross-Validation）の簡単な説明

交差確認（または交差検証、Cross-Validation）とは、データ分析手法の「良さ」を評価する方法のことです。交差確認は、機械学習・深層学習の手法の良さを評価するのにしばしば使われます。

交差確認（交差検証）とは

交差確認とは、以下の5つの手順によって、データ分析手法の「良さ」を評価する方法のことです。

具体的に交差確認を、回帰の問題に適用してみましょう。

回帰における交差確認の例

１．データを分割します。試しにデータを赤、青、緑の３グループに分割してみます。

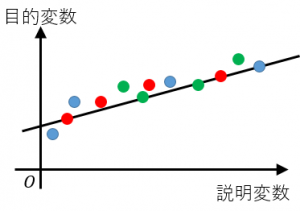
２．赤、青に特定の分析手法（例えば最小二乗法）を使って、データを表すそれっぽい直線（回帰式）を引いてみます。
関連：回帰分析の意味、嬉しさ、関連する用語

３．緑が回帰式でどれくらい説明できているのかを評価します。例えば、緑が直線からどれくらい離れているのかを二乗誤差などで評価します。この誤差を $e_g$ とします。

４．同様に、
赤と緑で回帰式を新たに作って、それを青で評価したときの誤差を $e_b$
青と緑で回帰式を新たに作って、それを赤で評価したときの誤差を $e_r$
とします。

５．「全体の誤差」として、例えば、誤差の平均
$e=\dfrac{1}{3}(e_g+e_b+e_r)$
を計算します。$e$ が小さいほど「回帰式の作り方が良い」（汎化性能が高いモデルを作成する分析手法である）と考えることができます。

K分割交差検証

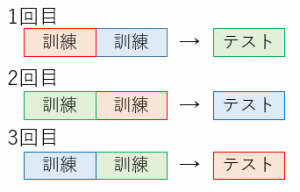
上の例のように
・データを $K$ 個に分割して、
・$K-1$ 個で訓練をして残りの $1$ 個でテストする
・というのを $K$ 回繰り返す
手法を $K$ 分割交差検証（K-fold クロスバリデーション）と言います。上の例では $K=3$ です。

データ量が十分でない場合でも、全てのデータを有効に活用できます。しかし、訓練とテストを $K$ 回行うため、計算時間がかかります。特に、$K$ が大きくなればなるほど大変です。

交差検証の他の方法

・交差確認は「分析アルゴリズムの（考えている問題に対する）良さ」を評価するための方法の一つです。回帰問題だけではなく、クラス分類問題にも使えます。
関連：クラス分類とクラスタリングの意味と違い

・分割のグループ数 $K$ がデータの個数と等しいとき、つまり、データを１つずつに分けて、データの個数と同じ回数だけ「訓練＋テスト」を行う場合を、特に、leave-one-out 交差検証と言います。leave-one-out の頭文字を使って LOO と表現することもあります。

・訓練用データとテスト用データへの分割の方法は、他にもバリエーションがあります。また、各テストでの誤差の評価方法や「全体の誤差」の評価方法にもバリエーションがあります。このように、一口に「交差確認」と言っても、いろいろな種類があるので、具体的に何をやっているのかは確認する必要があります。

次回は 確率的勾配降下法の大雑把な意味 を解説します。