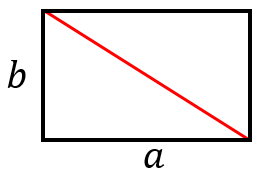
横の長さ $a$、縦の長さ $b$ の長方形について、
対角線の長さは $\sqrt{a^2+b^2}$
具体例
例題1
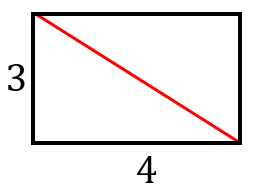
横の長さが $4$、縦の長さが $3$ の長方形の対角線の長さを計算せよ。
解答1
冒頭の公式より、対角線の長さは、
$\sqrt{4^2+3^2}=\sqrt{25}=5$
となります。
解答2
対角線の長さを $l$ とおきます。長方形の内角は全て直角なので、$\angle B$ は直角です。
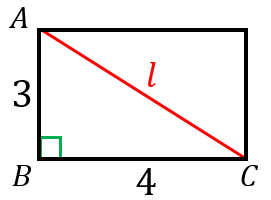
よって、三角形 $ABC$ は直角三角形なので、三平方の定理を使うと、
$l^2=3^2+4^2$
となります。これを計算していくと、
$l^2=9+16=25$
$l=\sqrt{25}=5$
公式の証明
上記の例題の解答2のように、三平方の定理を使うことで、どんな長方形でも、対角線の長さを求めることができます。
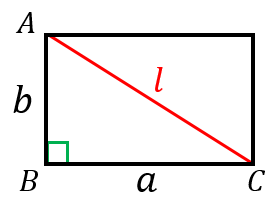
三角形 $ABC$ は直角三角形なので、三平方の定理を使うと、
$l^2=a^2+b^2$
となります。
よって、両辺のルートを取ると、
$l=\sqrt{a^2+b^2}$
となります。
この公式は上記のように簡単に導出することができるので、覚える必要はありません。「長方形の対角線の長さは三平方の定理を使うと求められる」と覚えておきましょう。
発展問題
例題2
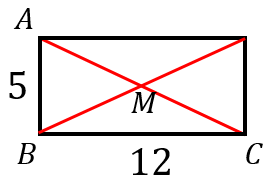
図のような長方形において、対角線の交点を $M$ とする。$AM$ の長さを求めよ。
解答
長方形の対角線はそれぞれの中点で交わります。
参考:平行四辺形、ひし形、長方形、正方形の違い
そのため、$AM=\dfrac{1}{2}AC$ となります。
対角線 $AC$ の長さが求まれば $AM$ の長さも分かります。
そこで、直角三角形 $ABC$ で三平方の定理を使うと、
$AC^2=5^2+12^2\\
=25+144\\
=169$
よって、$AC=13$
$AM=\dfrac{13}{2}$
まめ知識
長方形の横の長さ、縦の長さが整数でも対角線の長さが整数になるとは限りません。例えば、横の長さが $2$、縦の長さが $3$ の場合、対角線の長さは $\sqrt{2^2+3^2}=\sqrt{13}$ となります。
次回は 立方体と直方体の対角線の長さ を解説します。
