約分のやり方と計算ツール

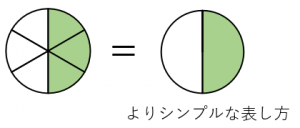
具体例

$\dfrac{3}{6}$ という分数は、分母も分子も $3$ の倍数なので、$3$ でわると、$\dfrac{1}{2}$ になります。つまり、$\dfrac{3}{6}$ を約分すると $\dfrac{1}{2}$ になります。（分母と分子を同じ数でわっても分数の値は変わりません、同じ分数を表すのならできるだけシンプルな形の方がよいですよね）

同様に、$\dfrac{20}{30}$ を約分する（分母と分子を $10$ でわる）と、$\dfrac{2}{3}$ になります。

関連：分数の計算の基本問題10問

約分計算ツール

分母と分子に正の整数を入力して「約分実行」を押すと約分されます。いろいろな分数で約分をしてコツをつかんでみてください！

約分のやり方（その1）

分母と分子が両方とも $2$ の倍数なら $2$ でわる
→分母と分子が両方とも $3$ の倍数なら $3$ でわる
→次は $5$、$7$、$11$
と順番にトライしていくことで必ず約分できます。

練習問題

$\dfrac{56}{140}$ を約分せよ。

答え

分母の $140$ も、分子の $56$ も $2$ でわれるので、
$\dfrac{56}{140}=\dfrac{28}{70}$
と約分できます。

さらに、分母の $70$ も、分子の $28$ も $2$ でわれるので、
$\dfrac{28}{70}=\dfrac{14}{35}$
と約分できます。

$35$ はこれ以上 $2$ でわれません。$3$ でもわれません。
次は $5$ をトライしますが、分子の $14$ は $5$ でわれません。
$7$ をトライしてみると、分母も分子も $7$ でわれます：
$\dfrac{14}{35}=$$\dfrac{2}{5}$
これが答えです。

多くの場合、$11$ くらいまで試せば約分は完了します。
順番に試していくのが素直ですが、慣れたら何でわればよいか直感で分かるようになります。たくさん約分してコツをつかんでください（上の約分ツールもご活用ください）！

約分のやり方（その2）

分母と分子の最大公約数で分母と分子をわれば、約分できます。

練習問題

$\dfrac{21}{30}$ を約分せよ。

答え

分母 $30$ の約数を並べると、$1,3,5,6,10,30$
分子 $21$ の約数を並べると、$1,3,7,21$
よって、最大公約数は $3$ である。分母と分子を $3$ でわると約分される：
$\dfrac{21}{30}$=$\dfrac{7}{10}$

ちなみに、約分の逆っぽい操作が通分です。

次回は 通分のやり方と練習問題 を解説します。