流量は「1秒あたりどれくらいの量が流れているか」を表します。
流速は「1秒あたりどれくらいの速さで流れているか」を表します。
流量と流速は、似ていますが、意味が違います。このページでは、流量や流速の意味と、変換方法について詳しく解説します。
流量とは
流量には体積流量と、質量流量の2種類があります。
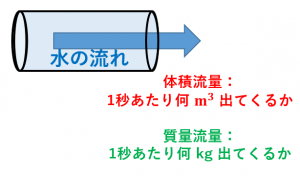
体積流量とは、単位時間あたりに流れる水の体積を表します。体積流量の単位としては、$\mathrm{m^3/s}$ などが使われます。
質量流量とは、単位時間あたりに流れる水の質量を表します。質量流量の単位としては、$\mathrm{kg/s}$ などが使われます。
※このページでは、「水」の例で説明しますが「水」の部分を「別の物質」に置き換えても同じ説明が成立します。
流速とは
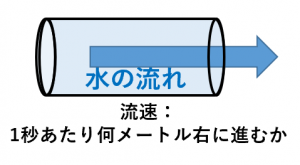
流速が大きいほど「水の勢いが速い」と言うことができます。
体積流量と流速の関係
体積流量$(\mathrm{m^3/s})$=断面積$(\mathrm{m^2})$$\times$流速$(\mathrm{m/s})$
という関係式が成立します。
例えば、断面積が $0.1\:\mathrm{m^2}$ である円柱を、流速 $0.3\:\mathrm{m/s}$ で流れている水について、体積流量は、$0.1\times 0.3=0.03\:\mathrm{m^3/s}$ のように計算できます。
関係式が成立する理由:
体積=断面積×移動距離
です。そのため、
「1秒あたりに流れた体積」=断面積×「1秒あたりの移動距離」
となります。つまり、
体積流量$(\mathrm{m^3/s})$=断面積$(\mathrm{m^2})$$\times$流速$(\mathrm{m/s})$
となります。
質量流量と流速の関係
流れた物質の質量と体積の間には、
質量=体積×密度
という関係が成立します。
参考:質量、密度、体積それぞれの求め方
よって、質量流量と体積流量の間には、
質量流量$(\mathrm{kg/s})$=体積流量$(\mathrm{m^3/s})$$\times$密度$(\mathrm{kg/m^3})$
という関係式が成立します。
先ほどの関係式と合わせると、
質量流量$(\mathrm{kg/s})$=断面積$(\mathrm{m^2})$$\times$流速$(\mathrm{m/s})$$\times$密度$(\mathrm{kg/m^3})$
となります。
流体が水の場合には、密度は(温度によって変化しますが)およそ $1000\:\mathrm{kg/m^3}$ なので、
質量流量$(\mathrm{kg/s})$=断面積$(\mathrm{m^2})$$\times$流速$(\mathrm{m/s})$$\times 1000$
が成立します。
次回は pH(ペーハー)の計算方法と4つのポイント を解説します。
