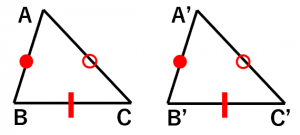
(i)3辺の長さがそれぞれ等しい
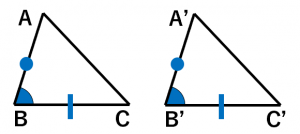
(ii)2辺とその間の角がそれぞれ等しい
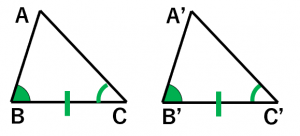
(iii)1辺とその両端の角がそれぞれ等しい
そもそも合同とは?
ただし「同じ形で同じ大きさ」とは平行移動や回転、裏返すことでピッタリ重なることを言います。
(i)3辺の長さがそれぞれ等しい
(ii)2辺とその間の角がそれぞれ等しい
(iii)1辺とその両端の角がそれぞれ等しい
のうちどれかが成り立つとき、2つの三角形は合同です。これらの条件のことを「三角形の合同条件」と言います。
合同であることの証明
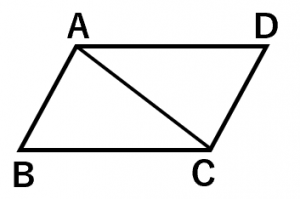
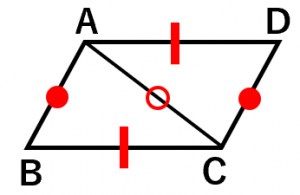
平行四辺形の向かい合う辺の長さは等しいです。よって、$AB=CD$、$BC=DA$ です。また、三角形 $ABC$ と三角形 $CDA$ で、辺 $AC$ は共通です。よって、3辺の長さがそれぞれ等しいので、三角形 $ABC$ と三角形 $CDA$ は合同になります。
直角三角形の合同条件
(a)直角三角形で、斜辺と他の1辺の長さがそれぞれ等しい
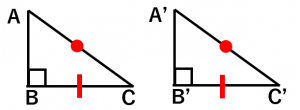
(b)直角三角形で、斜辺と1つの鋭角がそれぞれ等しい
直角三角形の合同条件は覚えていなくても、以下のように普通の三角形の合同条件を覚えていれば、合同であることを説明できます。
(a)について
条件(a)が成立するとき、3平方の定理より、残った1辺の長さも等しくなります。よって、2つの直角三角形は3辺の長さがそれぞれ等しいので、三角形の合同条件(i)により合同であることが分かります。
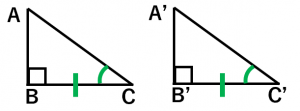
(b)について
条件(b)が成立するとき、三角形の内角の和は $180^{\circ}$ なので、残りの1つの角度も等しくなります。よって、2つの直角三角形は1辺とその両端の角がそれぞれ等しいので、三角形の合同条件(iii)により合同であることが分かります。
そのため、普通の三角形の合同条件(i)~(iii)は絶対覚える必要がありますが、直角三角形の合同条件(ii)は覚えなくても問題ありません。
次回は 三角形の相似条件と有名な例題3問 を解説します。
