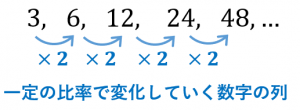
等比数列とは、一定の比率で変化していくような数列のことです。
このページでは、等比数列の意味、一般項の求め方、等比数列の和など、等比数列の知識を基礎から全て解説します。
等比数列とは
この一定の比率のことを等比数列の公比と言います。また、最初の数字のことを、等比数列の初項と言います。
例えば、$3,6,12,24,\cdots$ という数列は、初項が $3$ で公比が $2$ の等比数列です。
等比数列の公比の求め方
等比数列 $3,-1,\dfrac{1}{3},-\dfrac{1}{9},\dots$ の公比を求めてみましょう。
等比数列の公比は、適当な項÷その前の項で計算できます。
「適当な項」としては、どれを選んでも構いません。例えば、この例題の場合「適当な項」として、2番目の $-1$ を選ぶと、
公比は、$(-1)\div 3=-\dfrac{1}{3}$ のように計算できます。
等比数列の一般項とは

等比数列は、前の数字に公比をかけると次の数字になるので、
1番目の項は $3$
2番目の項は $3\times 2$
3番目の項は $3\times 2\times 2$
4番目の項は $3\times 2\times 2\times 2$
となります。つまり、$n$ 番目の項は、初項 $3$ に対して、$2$ を $(n-1)$ 回かけたものになります。よって、$n$ 番目の項を $a_n$ と書くと、$a_n=3\cdot 2^{n-1}$ と書くことができます。
このように、$n$ 番目の項 $a_n$ を $n$ を使って表した式のことを一般項と言います。
一般項を求める公式
初項が $a$ で、公比が $r$ である等比数列の一般項は、$a_n=ar^{n-1}$
先ほどの例題と同様に考えると、初項が $a$ で、公比が $r$ である等比数列の第 $n$ 項は、初項 $a$ に対して、$r$ を $(n-1)$ 回かけたものになります。よって、$a_n=ar^{n-1}$ になります。
もっと詳しく:等比数列の一般項の求め方の証明と例題
等比数列の和の計算例
初項が $3$ で公比が $2$ である等比数列 $3,6,12,24,\dots$ の、初項から $5$ 番目の項までの和を計算してみましょう。
$3+6+12+24+48$ を地道に計算しても良いですが、もう少し賢い方法があります。
まず、求めたい和を $S$ とおきます。
$S=3+6+12+24+48$
この式を $2$ 倍します:
$2S=\:\:6+12+24+48+96$
下の式から上の式を引くと、途中の $6$、$12$、$24$、$48$ が打ち消し合って、
$(2S-S)=-3+96$
となります。これを整理すると、
$S=93$
と和が求まりました。
等比数列の和の公式
初項が $a$ で、公比が $r$ である等比数列の、初項から $n$ 項目までの和は、
$S_n=\dfrac{a(r^n-1)}{r-1}$
ただし、$r\neq 1$ とします($r=1$ のときは、全ての項が $a$ であるつまらない数列です)。
この公式は、先ほどの例題と同様に証明できます。つまり、
$S=a+ar+\dots +ar^{n-1}$
という式と、これを $r$ 倍した式:
$rS=ar+\dots +ar^{n-1}+ar^n$
という式について両辺引き算をすると、途中の項が消えて
$S-rS=a-ar^n$
となります。これを $S$ について解くと、
$S=\dfrac{a(1-r^n)}{1-r}$
となります。
無限等比級数
等比数列の和を、ひたすら取っていった極限
$a+ar+ar^2+\cdots$
のことを無限等比級数と言います。
$a+ar+ar^2+\dots$
は $|r|<1$ のときに収束します。その値は $\dfrac{a}{1-r}$ となります。
これは、等比数列の和の公式で $n\to\infty$ の極限を取ることで証明できます。
もっと詳しく:
無限等比級数の公式の例題と証明
次回は 等比数列の一般項の求め方の証明と例題 を解説します。
