初項 $a$、公比 $r$ の等比数列の無限和:
$\displaystyle\sum_{n=1}^{\infty}ar^{n-1}=a+ar+ar^2+\cdots$
は、$|r|<1$ のとき、$\dfrac{a}{1-r}$ に収束する。
計算例
無限等比級数 $2+\dfrac{2}{3}+\dfrac{2}{9}+\dfrac{2}{27}+\cdots$ の値を求めよ。
$a=2$、$r=\dfrac{1}{3}$ として公式を使うと、
$\dfrac{2}{1-\frac{1}{3}}\\
=2\div \dfrac{2}{3}$
$=3$
となります。
公式の証明(式を使った説明)
$a+ar+ar^2+\cdots =\dfrac{a}{1-r}$
を証明してみましょう。
求めたいものは
$S=a+ar+ar^2+\cdots$
です。この式の両辺を $r$ 倍すると、
$rS=\:\:\:ar+ar^2+ar^3+\cdots$
となります。
上の式から下の式を引くと、
$S-rS=a+(ar-ar)+(ar^2-ar^2)+\cdots$
となり、右辺は $a$ 以外全て消えます。
つまり、
$S-rS=a$
$(1-r)S=a$
$S=\dfrac{a}{1-r}$
となります。
公式の証明(図形を使った説明)
次は、図形を使って
$a+ar+ar^2+\cdots =\dfrac{a}{1-r}$
を証明してみましょう。ただし、$0 < r < 1$ とします。

まず、面積 $a$ の長方形を $1-r:r$ に分けてみます。左側の面積は $a(1-r)$、右側の面積は $ar$ です。
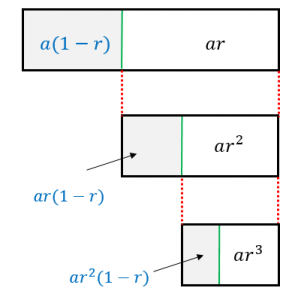
さらに右側の長方形を $1-r:r$ に分けてみます。
左側は $ar(1-r)$、右側は $ar^2$ です。
このように「右側を $1-r:r$ に分ける」という操作をいつまでも繰り返していくと、どんどん分割の緑のラインは右側に近づいていきます。
つまり、グレーの長方形の面積の和は限りなく $a$ に近づきます。これを式で表すと、
$a(1-r)+ar(1-r)+ar^2(1-r)+\cdots =a$
となります。この両辺を $1-r$ で割ると、
$a+ar+ar^2+\cdots =\dfrac{a}{1-r}$
となります。
図形の問題
半径 $r_n=\dfrac{1}{5^n}$ の円($n=1,2,\dots$)の面積 $S_n$ の和を求めよ。
半径 $r_n$ の円の面積は、
$S_n=\pi r_n^2=\dfrac{\pi}{25^n}$
です。よって、
$S_1+S_2+S_3+\cdots $
は初項が $S_1=\dfrac{\pi}{25}$、公比が $\dfrac{1}{25}$ の無限等比級数なので、答えは、
$\dfrac{\frac{\pi}{25}}{1-\frac{1}{25}}=\dfrac{\pi}{24}$
次回は x/e^x、x^2/e^xなどの極限の公式と証明 を解説します。
