$y=a^x$ という式で表される関数を指数関数と言います。
このページでは、指数関数の基本的な知識をまとめました。
指数関数の意味、身近な例、$x$ が整数でない場合の指数関数の値、指数関数のグラフ、定義域と値域という5つの項目について解説します。
指数関数とは
例えば、$y=2^x$ という指数関数について、
・$x=1$ とすると、$y=2^1=2$
・$x=2$ とすると、$y=2^2=4$
・$x=3$ とすると、$y=2^3=8$
・$x=4$ とすると、$y=2^4=16$
となります。
このように、指数関数では、$x$ が少し増えると $y$ がものすごい勢いで増えていくという性質があります。そのため「ものすごい増え方」のことを、指数関数的な増加と呼ぶことがあります。
関連:「指数的に増加」「指数関数的に増加」の意味
指数関数の身近な例
折り紙を何回も半分に折っていき、積み重なった紙の枚数を数えてきましょう。
・1回折ったときは2枚
・2回折ったときは4枚
・3回折ったときは8枚
となります。このように、$x$ 回折ったときの枚数を $y$ とすると、$y=2^x$ となります。指数関数が登場しました。
このように、指数関数は、倍々に増えていくような現象を表現するのに使えます。
$x$ が整数でないとき
・$x=\dfrac{1}{n}$ の場合
例えば $2^{\frac{1}{2}}=\sqrt{2}$、$2^{\frac{1}{3}}=\sqrt[3]{2}$ のように、$\dfrac{1}{n}$ が肩に載っているような指数は、$n$ 乗根で定義されます。
つまり、$x=\dfrac{1}{n}$ のとき、$y=\sqrt[n]{2}$ となります。
・$x=\dfrac{m}{n}$ の場合
有理数乗については、$2^{\frac{m}{n}}=\sqrt[n]{m}$ のように定義されます。
例えば、$x=\dfrac{3}{4}$ のとき、$y=\sqrt[4]{3}$ となります。
・$x$ が無理数の場合
無理数乗については、有理数乗の極限として定義されます。例えば、$x=\pi=3.1415\dots$ のときには、$2^3$、$2^{3.1}$、$2^{3.14}$ と順々に計算していき、近づいていく値のことを $2^{\pi}$ と定めます。
指数関数のグラフ
$a$ が $1$ より大きいとき、$y=a^x$ のグラフは、赤い曲線のようになります。
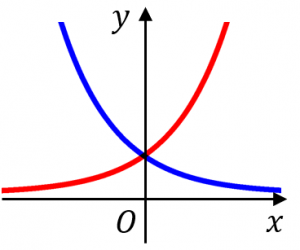
ポイントは、以下の4つです。
・$x=0$ のとき、$y=1$ となる
・$x=1$ のとき、$y=a$ となる
・右側ではものすごい勢いで増えていく
・左側では $0$ に近づいていく
$a$ が $1$ より小さいとき、$y=a^x$ のグラフは、青い曲線のようになります。
ポイントは、以下の4つです。
・$x=0$ のとき、$y=1$ となる
・$x=1$ のとき、$y=a$ となる
・左側ではものすごい勢いで増えていく
・右側では $0$ に近づいていく
指数関数の定義域、値域
指数関数のグラフからも分かるように、
・$y=a^x$ の定義域は、実数全体となります。
・$y=a^x$ の値域は、$y>0$ となります。
次回は 指数方程式とその解き方 を解説します。
