「指数的に」「指数関数的に」という単語はどちらも以下の2つの意味で使われることがあります。
意味1:
指数関数と同じくらいのペースで、ある量 $x$ の増加に伴って別の量 $y$ が急激に増加するという意味
意味2(厳密には正しくない):
単に急激に増加するという意味
意味1「指数関数と同じくらいのペースで増加する」
$2^1=2$
$2^2=4$
$2^3=8$
$2^4=16$
$2^{10}=1024$
$2^{20}=1048576$
というように、指数の数字(かけ算の回数)を増やしていくと、その値は急激に増加していきます。
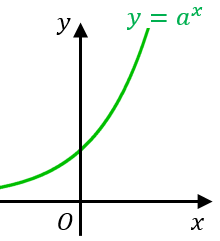
一般に、指数関数 $y=a^x$($a$ は $1$ より大きい定数)と同じくらいのペースで(ある量 $x$ の増加に伴って)$y$ が急激に増加するとき、その増加を「指数的な増加」または「指数関数的な増加」と言うことがあります。
例:
・売上が毎年、前年の約 $2$ 倍になっている。
・人口が毎月 $10$ %の割合で増加している。
・とある預金では年利 $1$ %の利子(複利)がつくため、お金が毎年増加する。
→これらは「指数的な増加」と言える。
「指数」は「一定量ずつ増えていく」よりも強い言葉です。「一定割合ずつ増えていく」「倍々ゲームで増えていく」というようなイメージです。
意味2「単に急激に増加する」
「単に急激に増加する」くらいの意味でしかないのに「指数的に増加する」という言葉が使われる場合があります。
例:$x$ と $y$ の関係をグラフで表したら図のようになった。これは右の方ですさまじい勢いで増えている。「指数関数的な増加」と言える!
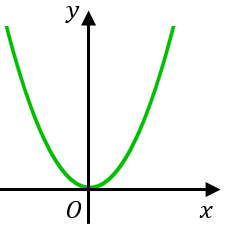
→実はこれは $y=x^2$ のグラフ。指数関数ではない。「二次関数的な増加」と言ったほうが正しい。
個人的には上記の例のような使い方は間違いだと思います。背後に何らかの指数関数が想定できるような場合以外は「指数的に」という言葉を使わずに、単に「急激に増加する」という言葉を使うべきだと思います。
ただし、意味2の使い方で指数的にという言葉を使う人がいるということは認識しておいてもよいでしょう。私は「指数的に増加する」と言われたときには「それは本当に指数関数のように増えるのか?」と考えるようにしています。
指数関数の増加スピードの凄まじさ
弱そうな指数関数:$y=1.01^x$
(毎回 $1$%ずつ増えていくようなイメージ)
強そうな二次関数:$y=100x^2$
を比較すると、一見、二次関数の方が増加のスピードが速そうです。しかし、実は $x$ をどんどん増やしていくと、$1.01^x$ の方が $100x^2$ よりもはるかに大きな値になります。
高校数学で習う極限を使うと、
$\displaystyle\lim_{x\to\infty}\dfrac{1.01^x}{100x^2}=\infty$
が成立します。
$x$ が小さいときにはあまり実感できませんか、長い目で見ると指数関数の増加は凄まじいものがあるのです。
次回は 半減期の意味と、典型的な計算問題3問を解説 を解説します。
