横の長さ $2a$、縦の長さ $2b$、質量 $M$ の一様な薄い長方形について、
重心を通り長方形に垂直な軸に関する慣性モーメントは、$\dfrac{1}{3}M(a^2+b^2)$
二重積分によって計算する方法
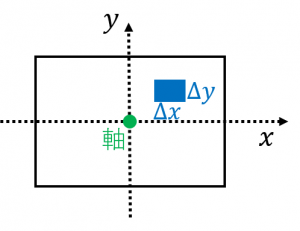
この微小な長方形の質量は、
$\Delta M=M\times\dfrac{\Delta x\Delta y}{2a\cdot 2b}$
です。
また、微小部分の、慣性モーメントへの寄与は、
$\Delta I=(x^2+y^2)\Delta M$
です。
よって、慣性モーメントは、
$I=\displaystyle\int_{-a}^a\int_{-b}^b(x^2+y^2)\times\dfrac{M}{4ab}dxdy\\
=\dfrac{M}{4ab}\displaystyle\int_{-a}^a\left[x^2y+\dfrac{y^3}{3}\right]_{-b}^bdx\\
=\dfrac{M}{2ab}\displaystyle\int_{-a}^a\left(x^2b+\dfrac{b^3}{3}\right)dx\\
=\dfrac{M}{ab}\left(\dfrac{a^3b}{3}+\dfrac{ab^3}{3}\right)\\
=\dfrac{M}{3}(a^2+b^2)$
となります。
平行軸の定理を使って計算する方法
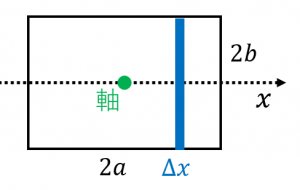
図の青い部分($x$ から $x+\Delta x$ の間にある、細い棒)は、重さが $\Delta M=\dfrac{M\Delta x}{2a}$ です。
そして、この一様な棒の「棒の重心を通り棒に垂直な軸に関する」慣性モーメントは、
$I_G=\dfrac{1}{12}(2b)^2\Delta M$
です。
関連:一様な棒の慣性モーメントの計算方法と考察
よって、この一様な棒の、長方形の慣性モーメントへの寄与は、平行軸の定理より、
$I_G+x^2\Delta M\\
=\left(\dfrac{b^2}{3}+x^2\right)\Delta M\\
=\dfrac{M}{2a}\left(\dfrac{b^2}{3}+x^2\right)\Delta x$
となります。これを積分すると、
$\dfrac{M}{2a}\displaystyle\int_{-a}^a\left(\dfrac{b^2}{3}+x^2\right)dx\\
=\dfrac{1}{3}M(a^2+b^2)$
公式の別の形
横の長さ $a$、縦の長さ $b$、の長方形の慣性モーメントは
$\dfrac{1}{12}M(a^2+b^2)$
1辺の長さ $a$、の正方形の慣性モーメントは、$\dfrac{1}{6}Ma^2$
※いずれも「質量 $M$ の一様な薄い」「重心を通り、垂直な軸に関する」慣性モーメントです。
次回は 平行軸の定理を分かりやすく説明【慣性モーメントの計算】 を解説します。
