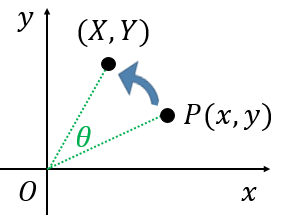
二次元座標平面上において、$(x,y)$ を原点中心に反時計回りに $\theta$ 回転させた点の座標 $(X,Y)$ は、以下の式で計算できる:
$\begin{pmatrix}X\\Y\end{pmatrix}=\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta &\cos\theta\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}$
具体例
例題
$(4,0)$ を原点中心に反時計回りに $60^{\circ}$ 回転させた点の座標を計算せよ。
解答
$\cos 60^{\circ}=\dfrac{1}{2}$、$\sin 60^{\circ}=\dfrac{\sqrt{3}}{2}$ なので、回転させた点 $(X,Y)$ は、
$\begin{pmatrix}X\\Y\end{pmatrix}=\begin{pmatrix}\cos 60^{\circ}&-\sin 60^{\circ}\\\sin 60^{\circ} &\cos 60^{\circ}\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}\\
=\begin{pmatrix}\frac{1}{2}&-\frac{\sqrt{3}}{2}\\\frac{\sqrt{3}}{2}&\frac{1}{2}\end{pmatrix}\begin{pmatrix}4\\0\end{pmatrix}\\
=\begin{pmatrix}2\\2\sqrt{3}\end{pmatrix}$
なお、行列の積については、行列の積の計算方法と例題をどうぞ。
余談:この回転の公式は、昔は高校数学で習っていました(行列の一次変換を高校数学で扱っていたのです)。
公式の証明
三角関数の加法定理を利用して、回転の公式を導出してみます。
まず、原点から $P$ までの距離を $r$、偏角を $\alpha$ とします(図参照)。すると、$x=r\cos\alpha$、$y=r\sin\alpha$ となります。
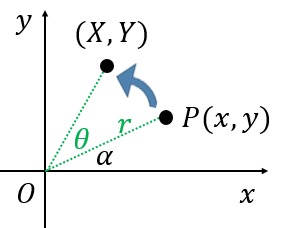
そして、コサインの加法定理を使うと、
$X=r\cos(\alpha+\theta)\\
=r\cos\alpha\cos\theta-r\sin\alpha\sin\theta\\
=x\cos\theta-y\sin\theta$
となります。同様に
$Y=r\sin(\alpha+\theta)\\
=r\sin\alpha\cos\theta+r\cos\alpha\sin\theta\\
=y\cos\theta+x\sin\theta$
この2つの式を行列の形で書くと、
$\begin{pmatrix}X\\Y\end{pmatrix}=\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta &\cos\theta\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}$
となります。
原点以外を中心とした回転の公式
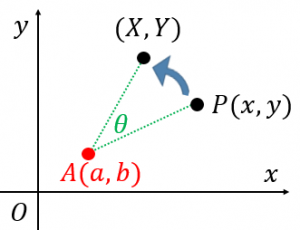
回転の中心が原点ではなく、$A(a,b)$ である場合については「ベクトル $AP$ を回転させる」と考えることで、以下のように同様の公式を得ることができます:
$\begin{pmatrix}X-a\\Y-b\end{pmatrix}=\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta &\cos\theta\end{pmatrix}\begin{pmatrix}x-a\\y-b\end{pmatrix}$
次回は 極座標における円の方程式の一般形と例題 を解説します。
