三角形の重心の定義といろいろな求め方

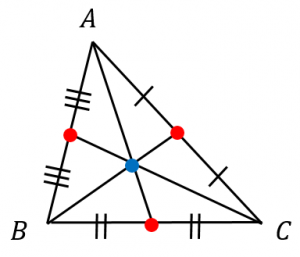
三角形の重心とは

～重心の定義２～
三角形の中線（３本あるが、どれでもよい）を $2:1$ に内分する点（頂点までの距離が2、中点までの距離が1）。

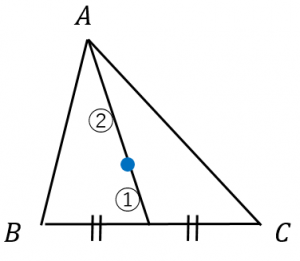
～重心の定義３～
均質な（重さに偏りがない）三角形のプレートを指一本で支えたとき、支えられる点。物理ではこの定義が分かりやすいかもしれません。

座標平面で重心を求める

～二次元座標平面における重心の求め方～
（平面上の）三角形 $ABC$ の各頂点の座標が $A(x_1,y_1)$、$B(x_2,y_2)$、$C(x_3,y_3)$ と与えられているとき、この三角形の重心の座標は $G\left(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3}\right)$ で求めることができます。

例題

$A(2,3)$、$B(-1,0)$、$C(2,6)$ のとき、三角形 $ABC$ の重心 $G$ の座標を求めよ。

解答

重心の座標を求める公式より、
$(\frac{2-1+2}{3},\frac{3+0+6}{3})$$=(1,3)$

～三次元座標空間における重心の求め方～
（空間上の）三角形 $ABC$ の各頂点の座標が $A(x_1,y_1,z_1)$、$B(x_2,y_2,z_2)$、$C(x_3,y_3,z_3)$ と与えられているとき、この三角形の重心の座標は $G\left(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3},\frac{z_1+z_2+z_3}{3}\right)$ で求めることができます。

位置ベクトルと重心

三角形 $ABC$ の各頂点の位置ベクトルが $A(\overrightarrow{a})$、$B(\overrightarrow{b})$、$C(\overrightarrow{c})$ と与えられているとき、この三角形の重心の位置ベクトルは、$\frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}$ となります。

複素数平面と重心

複素数平面における三角形 $ABC$ の各頂点に対応する複素数が $A(z_1)$、$B(z_2)$、$C(z_3)$ と与えられているとき、この三角形の重心に対応する複素数は、$\frac{z_1+z_2+z_3}{3}$ となります。

次回は 内分点と外分点の座標を求める公式 を解説します。