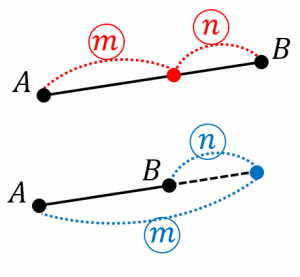
$A(a_x,a_y), B(b_x,b_y)$ を結ぶ線分を $m:n$ に内分する点の座標は、
$\left(\dfrac{na_x+mb_x}{m+n},\dfrac{na_y+mb_y}{m+n}\right)$
また、$m:n$ に外分する点の座標は、
$\left(\dfrac{-na_x+mb_x}{m-n},\dfrac{-na_y+mb_y}{m-n}\right)$
内分の具体例
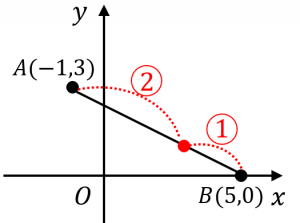
内分点の公式を使うと、内分点の座標は、
$\left(\dfrac{1\cdot(-1)+2\cdot 5}{2+1},\dfrac{1\cdot 3+2\cdot 0}{2+1}\right)\\
=\left(\dfrac{9}{3},\dfrac{3}{3}\right)$
$=(3,1)$
となります。
※ちなみに、内分点の公式で $m=n$ とすると、中点の座標を求める公式になります。
外分の具体例
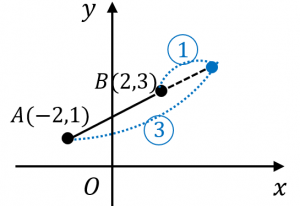
外分点の公式を使うと、外分点の座標は、
$\left(\dfrac{-1\cdot(-2)+3\cdot 2}{3-1},\dfrac{-1\cdot 1+3\cdot 3}{3-1}\right)\\
=\left(\dfrac{8}{2},\dfrac{8}{2}\right)$
$=(4,4)$
となります。
公式の覚え方
以下の3つの順番で考えると、公式を覚えやすいです。
内分の基本形は、 $\dfrac{nA+mB}{m+n}$ です。分子では $n,m$ の順に登場することに注意してください。
$\left(\dfrac{na_x+mb_x}{m+n},\dfrac{na_y+mb_y}{m+n}\right)$
$x$ 座標も $y$ 座標も同じ形なので、基本形だけ覚えておけばすぐに作ることができます。
$\left(\dfrac{-na_x+mb_x}{m-n},\dfrac{-na_y+mb_y}{m-n}\right)$
次回は 点と直線の距離の公式の意味と中学数学範囲での証明 を解説します。
