状態空間モデルとは、実際の状態を表す変数と実際に観測できる変数が異なるような系を数式で表現したものです。
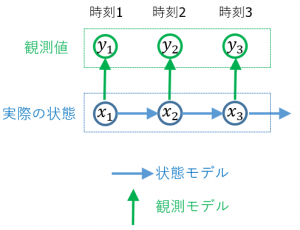
状態空間モデル(状態空間表現)は、気象の予測や制御理論など様々な応用があります。このページでは、状態空間モデルについて詳しく解説します。
状態空間モデルの簡単な例
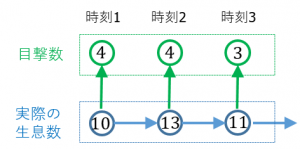
1.実際の状態を表す変数:
$t$ 年目における熊の生息数を $x_t$ とします。例では $x_1=10$、$x_2=13$、$x_3=11$ です。山の「状態」を表します。実際に何匹いるかは分かりません。$x_t$ のように、直接観測できないものの、実際の状態を表す変数のことを状態変数と言います。
2.実際に観測できる変数:
$t$ 年目における熊の目撃報告数を $y_t$ とします。例では $y_1=4$、$y_2=4$、$y_3=3$ です。$y_t$ は実際に集計できます。$y_t$ のように、直接観測できる変数を観測可能変数と言います。
3.状態モデル:
状態変数 $x_t$ が時刻 $t$ に依存してどう変化していくかを表現した式です。図では青色の矢印→に対応します。
例. $x_{t+1}=1.1x_t+v_t$
「何もしないと毎年熊は $1.1$ 倍ずつ増えていく。しかし、その増え方は確率的(例えば異常気象により生息数が激減するかもしれません)ので、確率変数 $v_t$ を使って表現する」というモデルです。
4.観測モデル:
状態変数 $x_t$ と観測可能変数 $y_t$ の間の関係式です。図では緑色の矢印↑に対応します。
$y_{t}=0.3x_t+w_t$
「熊の生息数の3割くらいの数の目撃情報が報告される。しかし、目撃数は確率的なので、確率変数 $w_t$ を使って表現する」というモデルです。
状態空間モデルを構成するもの

・$x_t$:状態変数(系の実際の状態を表す変数)
・$y_t$:実際に観測できる変数
・状態モデル:$x_{t+1}=f_t(x_t,v_t)$
・観測モデル:$y_{t}=g_t(x_t,w_t)$
分類1:線形 or 非線形
さきほどの例では状態変数も観測可能変数もスカラーでしたが、一般には多変量を扱うため、以下では $x_t$ や $y_t$ は(縦)ベクトルとしましょう。
・線形状態空間モデル
状態モデルおよび観測モデルが線形(一次式)で表現できるようなモデルです。行列 $A_t,B_t,C_t,D_t$ を用いて
$x_{t+1}=A_tx_t+B_tv_t$
$y_{t}=C_tx_t+D_tw_t$
($v_t$、$w_t$ は何かしらの確率分布に従う)
と表現できます。
・非線形状態空間モデル
線形でないものです。
分類2:正規 or 非正規
確率変数が従う分布が正規分布かどうかによっても分類することができます。
特に、正規かつ線形の状態空間モデルが(予測にカルマンフィルタという有名なアルゴリズムが使えるので)よく登場します:
$x_{t+1}=A_tx_t+v_t$
$y_{t}=C_tx_t+w_t$
($v_t$、$w_t$ は多変量正規分布に従う)
分類3:時不変 or 時変
・時不変状態空間モデル
状態モデルと観測モデルが時刻 $t$ に依存しないモデルです。
例えば、下記は「時不変かつ正規かつ線形の状態空間モデル」です:
$x_{t+1}=Ax_t+v$
$y_{t}=Cx_t+w$
($v$、$w$ は多変量正規分布に従う)
分類4:離散 or 連続
ここまでは離散の状態空間モデルを扱ってきましたが、連続の状態空間モデルも考えることができます。連続版は制御理論でしばしば使われます。
連続の場合は「一時刻後の値」などを考えられないので状態モデルは微分方程式で記述します。これを状態方程式と言います。
例えば、下記は「連続の時不変かつ線形の状態空間表現の例」です:
$\dfrac{dx(t)}{dt}=Ax(t)+Bu(t)$
$y(t)=Cx(t)+Du(t)$
ただし、$u(t)$ は確率変数ではなく制御入力(人間が決められる変数)で、状態方程式と観測方程式で共通としました。
なお、分野や人間によって用語の使い方が多少異なるので、この記事の用語の使い方は参考程度にしてくださいませ。
次回は 検査の評価指標(再現率、適合率、特異度、正確度、F値) を解説します。
