検査の評価指標（再現率、適合率、特異度、正確度、F値）

検査の手法がどれくらい優れているかを評価するための指標を整理しました。
病気の人は全員陽性、元気な人は全員陰性となる検査が理想ですが、実際にはそんなの不可能なので、「どれくらい正しいか」を評価する必要があります。

前提

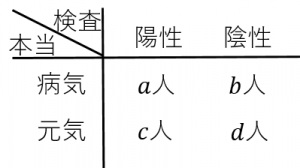
・$(a+b+c+d)$ 人に対して検査を行ったところ、図のような結果になった。
・$a$：真陽性（True Positive）
・$b$：偽陰性（False Negative）
・$c$：偽陽性（False Positive）
・$d$：真陰性（True Negative）
・$a$ と $d$ が多いほど「よい」検査、$b$ と $c$ が多いほど「悪い」検査。

なお、このページの指標はより一般に、二値分類モデル（検索システムなど）の評価指標として使えますが、ここでは病気の検査」という問題設定で考えます。

高いほどよい指標

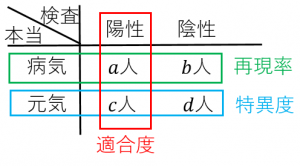
再現率（感度、真陽性率、Recall）
$\dfrac{a}{a+b}$：病気の人の中で検査で発見できる確率

適合率（精度、陽性反応的中度、Precision）
$\dfrac{a}{a+c}$：検査で陽性が出たときに実際に病気である確率

特異度（真陰性率、Specificity）
$\dfrac{d}{c+d}$：元気な人に対して、病気でないと判断する確率

正確度（Accuracy）
$\dfrac{a+d}{a+b+c+d}$：全体の中で正しく判断される割合

$F$ 値
$\dfrac{2}{\frac{1}{R}+\frac{1}{P}}=\dfrac{2a}{2a+b+c}$：再現率 $R$ と適合率 $P$ の調和平均（逆数の和の逆数の2倍）

低いほどよい指標

偽陰性率
$\dfrac{b}{a+b}$：病気の人に対して、検査で見逃してしまう確率

偽陽性率
$\dfrac{c}{c+d}$：病気でない人に対して、検査で病気とみなしてしまう確率

再現率と適合率のトレードオフ

たくさん陽性を出す検査（保守的な検査）は再現率は高くなりますが、適合率は低くなります。逆に、たくさん陰性を出す検査は適合率は高くなりますが、再現率は低くなります。つまり、再現率と適応度にはトレードオフの関係があります。

このため、再現率と適合度の両方を加味した指標である $F$ 値がしばしば使われます。

次回は マシューズ相関係数（Matthews Correlation Coefficient） を解説します。