絶対値：2つの意味と具体例

絶対値は中学数学の最初に習います。二つの考え方はどちらも同じです。分かりやすい方で覚えてください。

具体例

問題

(1) $3$ の絶対値を求めよ。
(2) $-7$ の絶対値を求めよ。
(3) $0$ の絶対値を求めよ。

解答

(1)
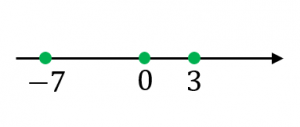
考え方I: 数直線上において $3$ と $0$ の距離は $3$ なので、$3$ の絶対値は $3$ です。
考え方II: $+3$ の符号をなくしても $3$ のままなので、$3$ の絶対値は $3$ です。

(2)
考え方I: 数直線上において $-7$ と $0$ の距離は $7$ なので、$-7$ の絶対値は $7$ です。
考え方II: $-3$ の符号をなくすと $7$ になるので、$-7$ の絶対値は $7$ です。

(3)
考え方I: 数直線上において $0$ と $0$ の距離は $0$ なので、$0$ の絶対値は $0$ です。
考え方II: $0$ の符号をなくしても $0$ のままなので、$0$ の絶対値は $0$ です。

次回は ルート（平方根）の意味と計算ツール を解説します。