全体集合と補集合の意味と公式

全体集合と補集合の意味と，関連する公式について紹介します。

全体集合とは

例えば、サイコロの出目について考えるとき、「考えている対象全体」は $U=\{1,2,3,4,5,6\}$ です。（出目は「1,2,3,4,5,6」の6通り）

全体集合のことを、英語で Universal Set と言うので、全体集合は $U$ という記号で表すことが多いです。

補集合とは

$A$ の補集合のことを $\overline{A}$ や、$A^{c}$ などと表すことが多いです。

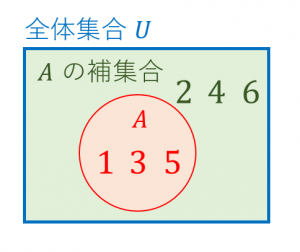
例えば、$U=\{1,2,3,4,5,6\}$ が全体集合で、$A=\{1,3,5\}$ のとき、$A$ の補集合は、$\overline{A}=\{2,4,6\}$ になります。

補集合のことを、英語で Complement と言うので、$A^{c}$ という記号を使うことがあります。

全体集合と補集合の要素数の公式

全体集合の要素数 $|U|$ と，補集合の要素数 $|\overline{A}|$ の間には，以下の公式が成立します。

例えば、人間の集合 $U$ に対して
$20$ 歳以上の人の集合を $A$ とすると、
補集合 $\overline{A}$ は $20$ 歳未満の人の集合になります。

$20$ 歳以上の人数
＋$20$ 歳未満の人数
＝人間全体の人数

なので、$|A|+|\overline{A}|=|U|$ が成立します。

ド・モルガンの法則

全体集合と補集合にまつわる重要な公式として，ド・モルガンの法則があります。

上の２つの公式を合わせて、ド・モルガンの法則と言います。

具体例で確認してみましょう。
$U=\{1,2,3,4,5,6\}$
$A=\{1,3,5\}$
$B=\{1,2,3\}$
としてみます。

・$\overline{A\cap B}=\overline{A}\cup \overline{B}$ の確認
$A\cap B=\{1,3\}$ なので、左辺は
$\overline{A\cap B}=\{2,4,5,6\}$
です。一方、
$\overline{A}=\{2,4,6\}$、$\overline{B}=\{4,5,6\}$
なので、$\overline{A}\cup \overline{B}=\{2,4,5,6\}$ です。

・$\overline{A\cup B}=\overline{A}\cap \overline{B}$ の確認
$A\cup B=\{1,2,3,5\}$ なので、左辺は
$\overline{A\cup B}=\{4,6\}$
です。一方、
$\overline{A}=\{2,4,6\}$、$\overline{B}=\{4,5,6\}$
なので、$\overline{A}\cap \overline{B}=\{4,6\}$ です。

次回は 集合の要素数についての２つの公式 を解説します。