集合の要素数についての２つの公式

集合の要素数を計算するときに使う公式を解説します。

２つの集合の要素数

ただし、集合 $A$ の要素数を $n(A)$ などと書きます。

この公式は、ベン図を使うと理解しやすいです。

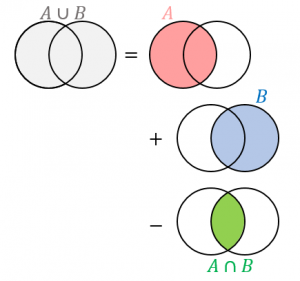
灰色の領域の要素数を数えるときに、
$n(A)$ と $n(B)$ を足し算すると、$A\cap B$ の部分を２回カウントしてしまっているので、１回分引く。
というイメージです。

例題

解答

$A$：田中さんの集合
$B$：太郎さんの集合
とします。$n(A)=5$、$n(B)=3$ です。

このとき、$A\cap B$ は、田中太郎さんの集合になります。よって、$n(A\cap B)=1$ です。

求めたいのは「田中」または「太郎」である人の数、つまり、$n(A\cup B)$ です。ここで公式を使うと、
$n(A\cup B)=n(A)+n(B)-n(A\cap B)\\
=5+3-1=7$
となります。

３つの集合の要素数

３つの場合は少し複雑です。

この公式も、ベン図を使って理解できます。

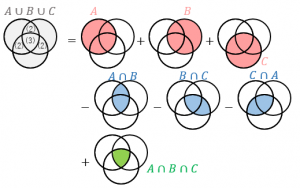
灰色の領域の要素数を数えるときに、
・とりあえず $n(A)$、$n(B)$、$n(C)$ を足し算する。すると、重なっている部分を複数回カウントしてしまう。具体的には、(2) の部分を２回、(3) の部分を３回カウントしてしまう。
・そこで、$n(A\cap B)$、$n(B\cap C)$、$n(C\cap A)$ を引き算することで、(2) の部分が１回のみカウントされるようにする。しかし、このとき、(3) の部分は３回カウントして、３回引き算したので、カウントできていない。
・そこで、最後に $n(A\cap B\cap C)$ を足し算することで、(3) の部分が１回カウントされるようにする。

次回は 部分集合と真部分集合の違い を解説します。