全反射とは、大雑把に言うと「屈折せずに全て反射する」現象のことです。このページでは、全反射の意味と、条件を分かりやすく解説します。また、臨界角の計算方法も紹介します。
全反射とは
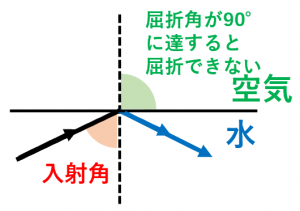
水中(下側)にある光源から空気(上側)の方に向かって光が出る状況を考えます。
一般的には、光は水面にぶつかると、空気の方に抜けるものと、反射して水の底側に戻るものとに分かれます。
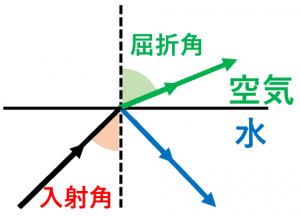
このとき、図のように、赤い角度よりも緑の角度の方が大きくなります。
赤い角度のことを入射角と言います。また、緑の角度のことを屈折角と言います。
そして、入射角をどんどん大きくしていくと、屈折角はどんどん大きくなり、遂には $90$ 度に達します。

このように、入射角が大きい状況では、空気の方に抜けるものが無くなり、反射して水の底側戻るもののみになります。このような現象のことを全反射と言います。
全反射の条件(大雑把な説明)
全反射は、
1. 入射角が屈折角より大きく
2. 入射角がある一定値より大きい
場合に起こります。
1についての詳細説明
入射角が屈折角より大きくなるのは、屈折率が大きい媒質から屈折率の小さい媒質に向けて進む場合です。そこで、有名な媒質を屈折率が小さい順に並べると、
空気<氷<水<エタノール<油<ダイヤモンド
となります。
水の方が空気より屈折率が大きいです。そのため、水から空気に進む光については全反射が起こりますが、空気から水に進む光については全反射は起こりません。
2について補足
計算上の屈折率が90度を超えるような場合に全反射が起こります。水から空気に進む光については、入射角が約49°より大きい場合に全反射が起こります。
全反射の条件(臨界角の計算)
「入射角が $\theta_0$ を超えたときに全反射が起こる」というような $\theta_0$ のことを臨界角と言います。
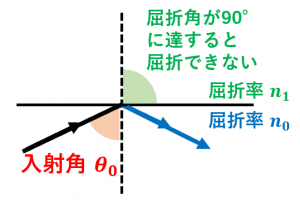
入射元の媒質の屈折率を $n_0$、行き先の媒質の屈折率を $n_1$ とすると、スネルの法則より、
$n_0\sin\theta_0=n_1\sin 90^{\circ}$
が成立します。これを整理すると、
$\sin\theta_0=\dfrac{n_1}{n_0}$
となります。
例えば、水から空気の場合には、$n_0=1.33$、$n_1=1.00$ として計算すると、
$\sin\theta_0=1.00\div 1.33\fallingdotseq 0.752$
$\theta_0\fallingdotseq 49^{\circ}$
となります。
まとめ
全反射は、
1. 入射角が屈折角より大きく
2. 入射角がある一定値 $\theta_0$ より大きい
場合に起こります。
そして、上記の $\theta_0$ のことを臨界角と言い、$\sin\theta_0=\dfrac{n_1}{n_0}$ を満たします。
次回は ベクトルの外積の定義、図形的な意味、微分の公式 を解説します。
