ベクトルの外積の定義、図形的な意味、微分の公式

このページでは，ベクトルの外積について，外積の計算方法，外積の図形的な意味，外積の微分などを詳しく解説します。

外積とは，2つの3次元空間ベクトル $(x_1,y_1,z_1)$、$(x_2,y_2,z_2)$ に対して
$x$ 成分が $y_1z_2-z_1y_2$
$y$ 成分が $z_1x_2-x_1z_2$
$z$ 成分が $x_1y_2-y_1x_2$
で計算されるようなベクトルのことです。

外積の計算例

$\overrightarrow{a}$ と $\overrightarrow{b}$ の外積を $\overrightarrow{a}\times \overrightarrow{b}$ と書きます。

外積の $x$ 成分は，
$y_1z_2-z_1y_2=2\cdot 6-3\cdot 5=-3$
外積の $y$ 成分は，
$z_1x_2-x_1z_2=3\cdot 4-1\cdot 6=6$
外積の $z$ 成分は，
$x_1y_2-y_1x_2=1\cdot 5-2\cdot 4=-3$

のように計算できます。

外積の図形的な意味

外積は，
与えられた2つのベクトルと直交し，
大きさが「もとの2つのベクトルが作る平行四辺形の面積」に等しい
ようなベクトルであることが知られています。それぞれ詳しく説明します。

外積はもとのベクトルに直交する

外積 $\overrightarrow{a}\times \overrightarrow{b}$ はもとのベクトル $\overrightarrow{a}$、$\overrightarrow{b}$ それぞれと直交する。
という性質があります。実際、先ほどの例では、
$(\overrightarrow{a}\times \overrightarrow{b})\cdot\overrightarrow{a}\\
=-3\cdot 1+6\cdot 2+(-3)\cdot 3=0$
$(\overrightarrow{a}\times \overrightarrow{b})\cdot\overrightarrow{b}\\
=-3\cdot 4+6\cdot 5+(-3)\cdot 6=0$
となり直交していることが確認できます。

つまり、二つの空間ベクトルが与えられたとき、それら両方ともに直交するベクトルを素早く求めるときに外積が使えるということになります。

外積の大きさは面積を表す

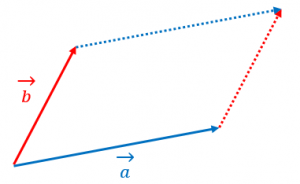
外積 $\overrightarrow{a}\times \overrightarrow{b}$ の大きさはもとのベクトル $\overrightarrow{a}$、$\overrightarrow{b}$ が張る平行四辺形（図参照）の面積と等しい。
という性質があります。

つまり、二つの空間ベクトルが与えられたとき、それらが張る平行四辺形の面積を素早く求めるときにも外積が使えるということになります。

ベクトルの外積と内積の違い

外積は，2つのベクトルに対してベクトルを対応させます。
内積は，2つのベクトルに対してスカラーを対応させます。

外積は，2つのベクトルが両方とも三次元の場合にのみ定義されます。
内積は，2つのベクトルの次元が等しければ何次元でも定義できます。

外積の微分公式

ベクトル解析の公式です（大学の力学、電磁気で使います）。
$\overrightarrow{a}$ と $\overrightarrow{b}$ が時刻 $t$ に依存するとき、外積 $\overrightarrow{a}\times \overrightarrow{b}$ の微分は、
$\dfrac{d(\overrightarrow{a}\times \overrightarrow{b})}{dt}=\dfrac{d\overrightarrow{a}}{dt}\times \overrightarrow{b}+\overrightarrow{a}\times \dfrac{d\overrightarrow{b}}{dt}$
で計算することができます。

積の微分公式を使って成分ごとに計算すれば証明できます。
関連：ベクトルの微分、ベクトルで微分

次回は LU分解のやり方と連立方程式を解くときのうれしさ を解説します。