行列 $A$ に対して、
$i$ 行と $j$ 列を除いた行列の行列式を $(-1)^{i+j}$ 倍したもの
のことを($ij$ 成分についての)余因子と言います。
また、余因子を並べた行列を余因子行列と言います。
余因子の例
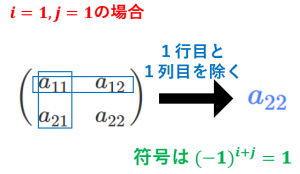
・$11$ 成分についての余因子
$A$ から $1$ 行目と $1$ 列目を除いた行列の行列式は、$a_{22}$ です。これに、符号 $(-1)^{1+1}=1$ をかけるので、$11$ 成分についての余因子は $a_{22}$ となります。
同様に、
・$12$ 成分についての余因子は、
$a_{21}$$\times$$(-1)^{1+2}$$=-a_{21}$
・$21$ 成分についての余因子は、
$a_{12}$$\times$$(-1)^{2+1}$$=-a_{12}$
・$22$ 成分についての余因子は、
$a_{11}$$\times$$(-1)^{2+2}$$=a_{11}$
となります。
よって、$ij$ 成分についての余因子を $ij$ 成分に並べると、
$\begin{pmatrix}a_{22}&-a_{21}\\-a_{12}&a_{11}\end{pmatrix}$
となります。
$3\times 3$ 行列の余因子
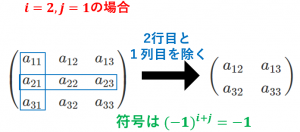
例えば、$21$ 成分についての余因子は
・$2$ 行目と $1$ 列目を除いた行列 $\begin{pmatrix}a_{12}&a_{13}\\a_{32}&a_{33}\end{pmatrix}$ の行列式 $a_{12}a_{33}-a_{13}a_{32}$ に
・$(-1)^{2+1}=-1$
をかけると、$-(a_{12}a_{33}-a_{13}a_{32})$
となります。
残り8個の余因子も同様に計算することができます。全て計算するのはそれなりに大変です。
余因子行列を実際に計算する方法
WolframAlphaにアクセスし、
cofactor matrix ({1,2,3},{4,5,6},{7,8,9})
と入力すれば、
$\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}$
の余因子行列を求めることができます。
余因子展開
$\displaystyle\sum_{j=1}^na_{ij}c_{ij}=\det A$
が成立します。ただし、$A$ は $n \times n$ 行列、$c_{ij}$ は $A$ の余因子行列の $ij$ 成分とします。
つまり、$i$ 行目の各要素について対応する余因子をかけて、全て足し合わせると行列式になります。
例えば、$A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}$ を $i=2$ 行目に関して余因子展開した式は、
$4c_{21}+5c_{22}+6c_{23}=\det A$
となります。ただし、
$c_{21}=-(2\times 9-3\times 8)$
$c_{22}=1\times 9-3\times 7$
$c_{23}=-(1\times 8-2\times 7)$
です。
つまり、全ての $j$($1\leq j\leq n$)に対して
$\displaystyle\sum_{i=1}^na_{ij}c_{ij}=\det A$
も成立します。
余因子行列と逆行列の関係
が成立します。
つまり、$\det A\neq 0$ の場合 $A^{-1}=\dfrac{1}{\det A}C^{\top}$ となります。
$A$ の逆行列は、余因子行列の転置 $C^{\top}$ の $\dfrac{1}{\det A}$ 倍と一致します。
なお、余因子展開、および逆行列との関係の証明は、以下のPDFファイルに分かりやすく記載されています。
余因子展開とその応用
次回は 対角行列の様々な性質(行列式や固有値など) を解説します。
