Q-QプロットとP-Pプロットについて整理しました。
Q-Qプロットとは
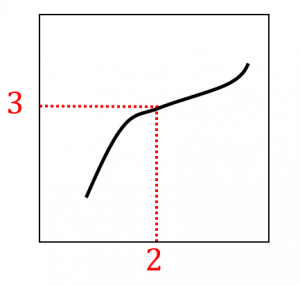
例えば、片方の分布の中央値($0.5$ 分位数)が $2$ で、もう片方の分布の中央値が $3$ であるとき、Q-Qプロットは $(2,3)$ を通ります。
このように、様々な $q\:(0\leq q\leq 1)$ に対して、
(片方の $q$ 分位数$,$もう片方の $q$ 分位数)
をプロットしたのがQ-Qプロットです。
Q-QプロットのQは分位数(Quantile)を表します。Q-Qプロットは単調非減少です。
Q-Qプロットの使い方
実際、2つの分布が一致するとき、全ての点は $y=x$ 上に乗ります。
つまり、Q-Qプロットが直線 $y=x$ に近い形になっていれば、2つの分布は似ている、と言うことができます。
例えば、よく分からないデータの分布と標準正規分布のQ-Qプロットを書くことで、データの分布が標準正規分布に従っているかどうかを、視覚的に確認することができます。(このような、ある分布が正規分布に従っているかを確認するためのプロットを正規確率プロットと言うことがあります)
P-Pプロットとは
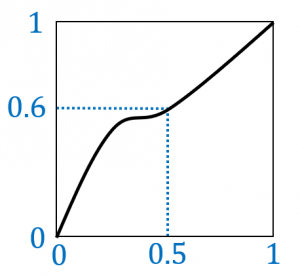
例えば、片方の分布について値が $3$ 以下である確率が $0.5$ で、もう片方の分布について値が $3$ 以下である確率が $0.6$ であるとき、P-Pプロットは $(0.5,0.6)$ を通ります。
このように、様々な $a$ に対して、
(片方の分布で値が $a$ 以下になる確率$,$もう片方の分布で値が $a$ 以下になる確率)
をプロットしたのがP-Pプロットです。
横軸と縦軸は確率なので、範囲は $0$ 以上 $1$ 以下です。P-Pプロットも単調非減少です。
P-Pプロットの使い方
「Q-Qプロットの使い方」で述べたQ-Qプロットの性質は、全てP-Pプロットにも当てはまります。つまり、P-Pプロットも、2つの分布が似ているかどうかを視覚的に確認するために使えます。
P-PプロットとQ-Qプロットの違い
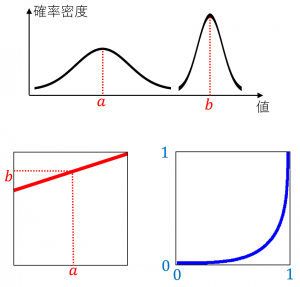
・Q-Qプロットは直線になります。
・P-Pプロットは直線にはなりません。
このように「同じ種類」の2つの分布について、Q-Qプロットは直線になりますが、P-Pプロットは一般には直線になりません。
(平行移動と定数倍で変換できる分布を「同じ種類」の分布と呼ぶことにしました)
したがって、
2つの分布が一致しているかどうかを確認したいときは、Q-QプロットまたはP-Pプロットが $y=x$ っぽいかどうかで判断できて、
2つの分布が「同じ種類」の分布なのかどうかを確認したいときは、Q-Qプロットが直線っぽいかどうかで判断できます。
参考文献:Comparison of P-P Plots and Q-Q Plots
次回は データの正規化(最大値・最小値バージョン、平均・分散バージョン) を解説します。
