チェバの定理:
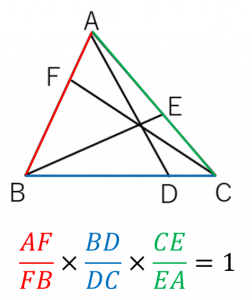
・三角形 $ABC$ と、その辺上の点 $D,E,F$ がある
・$AD,BE,CF$ は一点で交わる
このとき、$\dfrac{AF}{FB}\times\dfrac{BD}{DC}\times\dfrac{CE}{EA}=1$
が成立します。これをチェバの定理と言います。
チェバの定理の覚え方
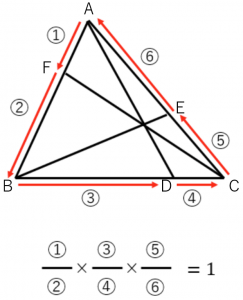
図のように
三角形の好きな頂点からスタートして、辺をつたって一周たどる。その順番に分数を書いていく
(分子→分母→分子→分母→分子→分母)
すると、チェバの定理:$\dfrac{AF}{FB}\times\dfrac{BD}{DC}\times\dfrac{CE}{EA}=1$ が得られます。
チェバの定理の例題
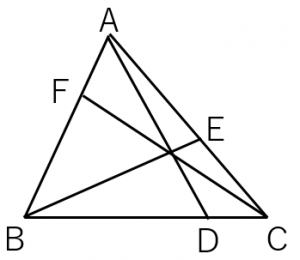
図において、$AF:FB=1:2$、$BD:DC=3:1$ とする。このとき、$CE:EA$ を求めよ。
解答
与えられた条件より、$\dfrac{AF}{FB}=\dfrac{1}{2}$、$\dfrac{BD}{DC}=3$ である。これらをチェバの定理:$\dfrac{AF}{FB}\times\dfrac{BD}{DC}\times\dfrac{CE}{EA}=1$
に代入すると、
$\dfrac{1}{2}\times\dfrac{3}{1}\times\dfrac{CE}{EA}=1$
よって、$\dfrac{CE}{EA}=\dfrac{2}{3}$
つまり、$CE:EA=2:3$
チェバの定理はこの問題のように「辺の比が二つ与えられたとき、3つめの辺の比を求めよ」という形で出題されることが多いです。
チェバの定理の証明
三角形の面積比を用いた証明が有名です。三角形 $APB$ の面積を $S(APB)$ と表記することにします。
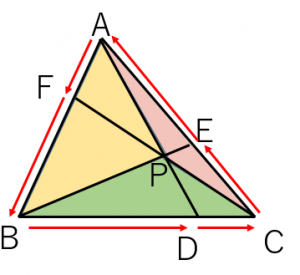
底辺 $CP$ を共通に持つ三角形の面積比を考えると、
$S(APC):S(BPC)=AF:FB$
が成立します。同様に、
$S(APB):S(APC)=BD:DC$
$S(BPC):S(APB)=CE:EA$
これらを分数の形で表現すると、
$\dfrac{S(APC)}{S(BPC)}=\dfrac{AF}{FB}$
$\dfrac{S(APB)}{S(APC)}=\dfrac{BD}{DC}$
$\dfrac{S(BPC)}{S(APB)}=\dfrac{CE}{EA}$
これら3つの式をかけ合わせると、左辺は $1$ になり、右辺は $\dfrac{AF}{FB}\times\dfrac{BD}{DC}\times\dfrac{CE}{EA}$ となります。これにてチェバの定理が証明されました。
チェバの定理の逆

実は、チェバの定理の逆も成立します。つまり、
三角形 $ABC$ と、各辺上の点 $D$、$E$、$F$ について、$\dfrac{AF}{FB}\times\dfrac{BD}{DC}\times\dfrac{CE}{EA}=1$ が成立するとき、三直線 $AD$、$BE$、$CF$ は一点で交わります。
次回は 三角形の内心の証明と頻出例題2問 を解説します。
