月の重力が地球の1/6になる理由と豆知識

月の重力はなぜ地球の1/6になるのか？
その理由を万有引力の法則から厳密に説明し、さらに「月で物体を落とすとどうなるか」「月で投げる・ジャンプするとどうなるか」という具体的なイメージもわかりやすく解説します。

月の重力は地球の1/6 ― その意味と直感的イメージ

重力が小さいほど、物体はゆっくり落下します。
そのため「1/6の重力がどれほど小さいのか」を理解するには、落下スピードを比較すると直感的です。

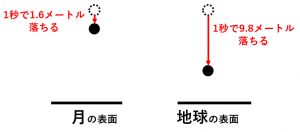
● 月の重力加速度： 約 $1.6\:\mathrm{m/s^2}$
　→ 1秒後に約1.6 m 落下
● 地球の重力加速度： 約 $9.8\:\mathrm{m/s^2}$
　→ 1秒後に約9.8 m 落下（空気抵抗無視）

比べると、月では落下スピードが非常にゆっくりであることが分かります。

なぜ月の重力は地球の1/6？ ― 万有引力の法則から説明

万有引力の法則より、天体の重力加速度は

– 天体の質量に比例
– 半径の2乗に反比例

します。

地球と月の比較データを見ると，

– 地球の質量：月の$81.3$ 倍
– 地球の半径：月の$3.67$ 倍

よって重力の比は、

\[
\frac{81.3}{3.67^2} \approx 6.0
\]

つまり、地球の重力は月の約6倍であり、「月の重力が地球の1/6」という結論に到達します。

—

※補足：万有引力から導かれる式

重力加速度 $g$ は、

\[
g = G \frac{M}{r^2}
\]

となり、
– 質量 $M$ に比例
– 半径 $r$ の二乗に反比例

という性質が明確に分かります。

月でボールを投げると？ジャンプすると？

例えば、地球でボールを投げて10 m 到達する場合、月で同じ力で投げると約60 m まで上昇します。

また、月でジャンプすると、理論的には地球の6倍の高さまで跳べます。

例：
地球で 50 cm ジャンプできる人
→ 月では 約 3 m ジャンプ可能

※空気抵抗は無視。宇宙服の影響で実際には地球と同じパワーを出しにくい点に注意。

月の重力に関するFAQ

Q1. 月で走ると速くなる？

A. 重力が小さいため跳躍距離は伸びますが、摩擦が小さいので加速はしにくく、単純に「速く走れる」とは言えません。

Q2. 月で物を落とすと、地球のように「加速して落ちる」？

A. はい。重力加速度は小さいですが、地球と同じく自由落下が起こります。

Q3. 月の重力が1/6なのに、大気はないの？

A. 1/6の重力では、大気を引き留めておく力が弱く、大気は宇宙空間に逃げてしまいました。これが月に空気がない主な理由です。

まとめ：月の重力が1/6である理由を理解すると宇宙が身近になる

● 月の重力は地球の1/6
● 理由は
・質量の小ささ
・半径の小ささ
により、重力加速度が大幅に小さくなるため
● 月では物体の落下・投げ上げ・ジャンプがすべてスローモーションのようになる

宇宙や天体の運動を理解するうえで、月の重力はとても良い題材です。

次回は 第一宇宙速度と第二宇宙速度の意味と導出 を解説します。