等差数列の和を計算する2つの公式

このページでは、等差数列の和の公式を２種類紹介します。また、等差数列の和の公式を、図を使って証明します。

公式１の例

まずは、等差数列の和の公式１を使って例題を解いてみましょう。

例題１

$3+5+7+9+11$ を計算せよ。

答え１
足し算を頑張れば答えが $35$ であることは分かります。

答え２（等差数列の和の公式を使う方法）
初項 $3$、末項 $11$、項数 $5$ の等差数列の和なので、公式１：$\dfrac{n}{2}(a+l)$ より、
$\dfrac{5}{2}(3+11)=\dfrac{5}{2}\times 14=35$
と計算することができます。

答え３
求めたい和を $S$ とおきます。

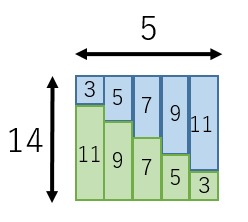
$S=3+5+7+9+11$
$S=11+9+7+5+3$
という2つの式の両辺をそれぞれ縦に加えると、
$2S=14+14+14+14+14$
となります。
よって、$2S=14\times 5=70$、$S=35$ となります。

公式１の証明

次に、等差数列の和の公式１を証明してみましょう。

すなわち、求めたい和を $S$ とおき、
$S=a+(a+d)+\cdots +(l-d)+l$
$S=l+(l-d)+\cdots +(a+d)+a$
という2つの式の両辺をそれぞれ縦に加えると、
$2S=(a+l)+(a+l)+\cdots +(a+l)$
となります。
よって、$2S=(a+l)\times n$、$S=\dfrac{n}{2}(a+l)$ となります。

公式２の例

等差数列の和の公式２についても例題を解いてみましょう。

例題２

初項が $a=6$、項差が $d=3$、項数が $n=4$ である等差数列の和を計算せよ。

解答

公式２：$\dfrac{n}{2}\{2a+(n-1)d\}$ より、等差数列の和は
$\dfrac{4}{2}\{2\cdot 6+(4-1)\cdot 3\}\\
=2\cdot(12+9)\\
=42$

２つの公式の関係

まず、末項 $l$ は初項、交差、項数を用いて $l=a+(n-1)d$ と表せます。

これを、公式：$\dfrac{n}{2}(a+l)$ に代入すると、$\dfrac{n}{2}\{a+a+(n-1)d\}$ となり、公式２になります。つまり、公式１から公式２を導くことができます。同様に、公式２から公式１も簡単に導けます。よって、公式１と公式２のどちらか１つだけを覚えれば十分です。（公式１を覚えるのがおすすめです）

次回は 和の記号シグマの意味と計算方法 を解説します。