点と直線の距離の公式の意味と中学数学範囲での証明

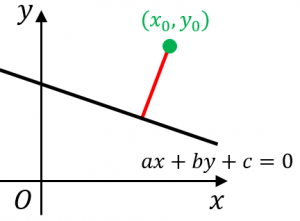
このページでは、点と直線の距離を計算する公式、および点と直線の距離の公式を使う例題、そして中学数学の範囲で分かる証明を解説します。

点と直線の距離とは

そもそも点 $P$ と直線 $l$ の距離とは、$P$ から、$l$ に下ろした垂線の足 $H$ までの距離 $PH$ のことを言います。

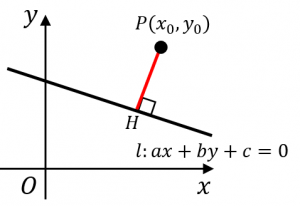
点 $P$ が直線 $l$ からどれくらい離れているかを表します。

点と直線の距離の公式を使う例題

点 $(x_0,y_0)$ と直線 $ax+by+c=0$ の距離は、$d=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$
でした。この公式に代入すると、
$d=\dfrac{|3\cdot 2-2\cdot 1+4|}{\sqrt{3^2+(-2)^2}}=\dfrac{8}{\sqrt{13}}$
と計算できます。

点と直線の距離の公式の証明

証明の計算は長いですが、中学数学の範囲で完結します。

まず、垂線の足 $H$ の座標を $(s,t)$ とおきます。$H$ は直線上にあるので、
$as+bt+c=0$ です。これを $t$ について解くと、
$t=-\dfrac{a}{b}s-\dfrac{c}{b}$
となります。

一方、$l$ は $y=-\dfrac{a}{b}x-\dfrac{c}{b}$ と変形できるので、傾きは $-\dfrac{a}{b}$ です。よって、垂直条件「傾きの積が $-1$」 を使うと、
$\dfrac{y_0-t}{x_0-s}\cdot\left(-\dfrac{a}{b}\right)=-1$
となります。この式を整理すると、
$(y_0-t)a=(x_0-s)b$
となります。この式に青色の式を代入すると、
$ay_0-a\left(-\dfrac{a}{b}s-\dfrac{c}{b}\right)=x_0b-sb$
これを $s$ について解いていきます：
$\dfrac{a^2}{b}s+bs=-ay_0+bx_0-\dfrac{ac}{b}$
$s=\dfrac{-aby_0+b^2x_0-ac}{a^2+b^2}$

よって、点と直線の距離は緑色の式も使うと、
$\sqrt{(x_0-s)^2+(y_0-t)^2}\\
=\dfrac{1}{a}\sqrt{a^2(x_0-s)^2+a^2(y_0-t)^2}\\
=\dfrac{1}{a}\sqrt{a^2(x_0-s)^2+b^2(x_0-s)^2}\\
=\dfrac{1}{a}|x_0-s|\sqrt{a^2+b^2}\\
=\dfrac{1}{a}\left|\dfrac{aby_0+a^2x_0+ac}{a^2+b^2}\right|\sqrt{a^2+b^2}\\
=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$
となります。

証明の補足

$a=0$ または $b=0$ の場合には、証明の途中式の分母が $0$ になるところがあるため、厳密にきちんと証明するためには場合分けが必要です。
（$a=0$ または $b=0$ の場合の証明は難しくありません）

高校数学で習うベクトルを使えば、場合分けをせずにスッキリ証明することができます。このページでは中学数学の範囲で理解できる証明をめざしたため、計算が少し複雑になりました。

次回は 円の方程式の求め方と例題4問 を解説します。