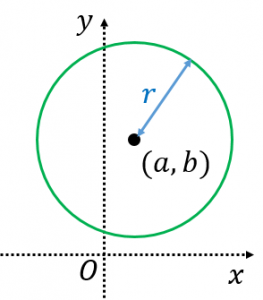
中心が $(a,b)$ で半径が $r$ の円の方程式は、$(x-a)^2+(y-b)^2=r^2$
特に、中心が原点で半径が $r$ の円の方程式は、$x^2+y^2=r^2$
簡単な例題3問
(1) $xy$ 座標平面上において、中心が原点、半径が $3$ の円を表す方程式を求めよ。
解答:冒頭の公式より、求める円の方程式は、$x^2+y^2=3^2$
つまり、$x^2+y^2=9$
(2) $xy$ 座標平面上において、中心が $(2,3)$、半径が $5$ の円を表す方程式を求めよ。
解答:冒頭の公式より、求める円の方程式は、$(x-2)^2+(y-3)^2=5^2$
つまり、$(x-2)^2+(y-3)^2=25$
※左辺を展開する必要はありません。
(3) $xy$ 座標平面上において $(x+1)^2+(y-2)^2=13$ という方程式が表す図形は何か?
解答:冒頭の公式を逆に使うと、$(x+1)^2+(y-2)^2=(\sqrt{13})^2$ は中心が $(-1,2)$ で半径が $\sqrt{13}$ の円を表すことが分かります。
与えられた2点を直径とする円の方程式
(4) $xy$ 座標平面上において $A(-3,2)$ と $B(1,4)$ を直径の両端とする円の方程式を求めよ。
解答:
円の中心と半径が分かれば円の方程式が求まります。
まず、円の中心は $AB$ の中点なので、その座標は $(\frac{-3+1}{2},\frac{2+4}{2})=(-1,3)$
また、半径は、
$\frac{1}{2}AB=\frac{1}{2}\sqrt{(1-(-3))^2+(4-2)^2}\\
=\frac{1}{2}\sqrt{16+4}\\
=\sqrt{5}$
よって、求める円の方程式は、円の方程式を求める公式より、
$\{x-(-1)\}^2+(y-3)^2=(\sqrt{5})^2$
つまり、
$(x+1)^2+(y-3)^2=5$
冒頭の公式の証明
中心が $(a,b)$ で半径 $r$ の円の方程式が、$(x-a)^2+(y-b)^2=r^2$ であることを証明します。
~証明~
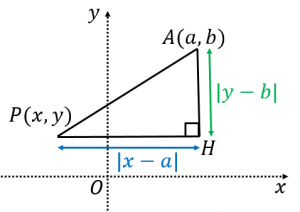
中心が $(a,b)$ で半径が $r$ の円上に点 $(x,y)$ がある
$\iff$ $(x,y)$ と $(a,b)$ の距離が $r$
$\iff$ $(x-a)^2+(y-b)^2=r^2$
となります。
ただし、最後の $\iff$ は三平方の定理を使いました(図で $PH^2+AH^2=AP^2$ が成立します)。
つまり、$(x-a)^2+(y-b)^2=r^2$ を満たす点 $(x,y)$ 全体は、中心が $(a,b)$ で半径が $r$ の円を表します。
次回は 3点を通る円の方程式の2通りの求め方と検算方法 を解説します。
