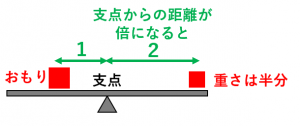
てこの原理に関連する計算を分かりやすく解説

てこの原理に関連する計算のやり方を詳しく解説します。棒の重さがある場合の計算方法も紹介します。

てこの原理の基本

よって、シーソーがつり合う状況では、支点からの距離が2倍になると、力の大きさ(おもりの重さ)は半分になります。

逆に、力の大きさが2倍になると、支点からの距離は半分になります。

すなわち、支点からの距離は、力の大きさに反比例するとも言えます。

てこの原理で重さを計算

回転させる能力
＝支点からの距離 $\times$ 力の大きさ
という公式を使って、つり合う場合の重さや距離を計算することができます。

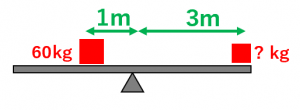
解答1：小学生でも分かる計算方法：
左側と右側で、支点からの距離 $\times$ 力の大きさ　が同じになるときに釣り合います。

つまり、つり合うとき、支点からの距離が○倍になると、重さは1/○倍になります。

今回は、右側は左側より支点からの距離は3倍です。よって、重さは左側の $\dfrac{1}{3}$ 倍になります。

よって、右側の重さは、
$60\times\dfrac{1}{3}=20\:\mathrm{kg}$
になります。

解答2：中学数学を使った計算方法：
右側の重さを $x\:\mathrm{kg}$ とすると、左右で
支点からの距離 $\times$ 力の大きさ
が等しいので、
$1\times 60=3\times x$
これを解くと、$x=20\:\mathrm{kg}$
となります。

棒の重さがある場合の計算

棒に重さがある場合は、棒の重心（中心）に、力が働いていると考えて計算します。

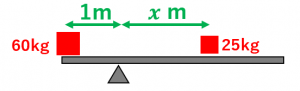
左側のおもりが反時計まわりに回転させる能力は、
$60\times 1$
です。

右側のおもりが時計まわりに回転させる能力は、
$25\times x$
です。

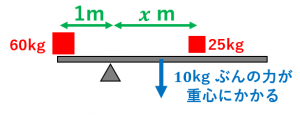
そして、棒の重さは、$10\:\mathrm{kg}$ ぶんの力が重心に働くと考えられるので、時計まわりに回転させる能力は、
$10\times 1$
です（棒の長さは4mなので、支点から重心までの距離は1mです）。

よって、つり合うとき、
$60\times 1=25\times x+10\times 1$

これを解くと、$x=2$ となります。

次回は ご飯とお米の重さの換算方法と便利ツール を解説します。