マルコフ連鎖の定常分布と極限分布について紹介します。
定常分布とは
マルコフ連鎖の遷移確率行列を $P$ とするとき、$\pi P=\pi$ を満たす(確率ベクトル)$\pi$ を定常分布と言います。
例題:図のような3つの状態からなるマルコフ連鎖の定常分布を計算せよ。
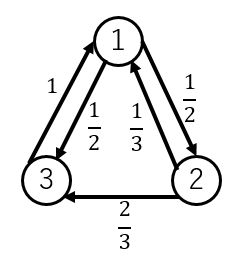
解答:
遷移確率行列は、
$P=\begin{pmatrix}0&\frac{1}{2}&\frac{1}{2}\\\frac{1}{3}&0&\frac{2}{3}\\1&0&0\end{pmatrix}$
となります。
求める定常分布を $\pi=(a,b,c)$ とすると、$\pi P=\pi$ なので、
$\dfrac{1}{3}b+c=a$
$\dfrac{a}{2}=b$
$\dfrac{a}{2}+\dfrac{2}{3}b=c$
となります。この連立方程式の解は、
$(a,b,c)=\left(t,\dfrac{t}{2},\dfrac{5}{6}t\right)$
(ただし、$t$ は任意の実数)となります。
ここで、$\pi$ は確率ベクトルなので、成分の和は $1$ になります:
$t+\dfrac{t}{2}+\dfrac{5}{6}t=1$
これを解くと、$t=\dfrac{3}{7}$ となります。
よって、定常分布は、
$\pi=\left(\dfrac{3}{7},\dfrac{3}{14},\dfrac{5}{14}\right)$
となります。
極限分布とは
任意の確率ベクトル $s$ に対して、
$\displaystyle\lim_{n\to\infty}sP^n=t$
となる確率ベクトル $t$ が存在するとき、$t$ を極限分布と言います。
実は、先ほどの例題において、
$\pi=\left(\dfrac{3}{7},\dfrac{3}{14},\dfrac{5}{14}\right)$
は極限分布にもなっています。
定常分布と極限分布の関係
$\displaystyle\lim_{n\to\infty}sP^n=t$
なら、$tP=t$ となります。
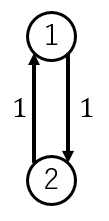
例えば、図のような周期的なマルコフ連鎖では、
・定常分布は $\pi=\left(\dfrac{1}{2},\dfrac{1}{2}\right)$ となります。
・初期状態として、$s=(1,0)$ とすると、$(0,1)$ と $(1,0)$ を交互に繰り返して収束しないので、極限分布は存在しません。
次回は 1e5、1e-6、1E+9などの数値の意味と注意点 を解説します。
