三角関数の周期について、基本となる公式を確認し、周期を求める例題を解説します。
基本となる公式
$y=\sin x$ の周期は $2\pi$
$y=\cos x$ の周期は $2\pi$
$y=\tan x$ の周期は $\pi$
です。確実に覚えましょう。
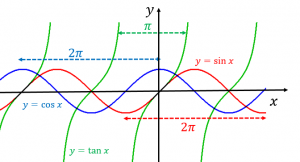
実際、グラフを見ると、$\sin x$ と $\cos x$ は $2\pi$ ごとに繰り返しており、$\tan x$ は $\pi$ ごとに繰り返していることが分かります。
y=sin 2x などの周期
$x$ の前に係数 $k$ がついている三角関数の周期は $\dfrac{1}{k}$ 倍になります。
つまり、
$y=\sin kx$ の周期は $\dfrac{2\pi}{k}$
$y=\cos kx$ の周期は $\dfrac{2\pi}{k}$
$y=\tan kx$ の周期は $\dfrac{\pi}{k}$
となります。
例題
(1) $y=\sin 2x$
(2) $y=\cos \dfrac{x}{3}$
(3) $y=\tan 4x$
の周期をそれぞれ求めよ。
答え
公式より、
(1) $y=\sin 2x$ の周期は $\dfrac{2\pi}{2}=\pi$
(2) $y=\cos\dfrac{x}{3}$ の周期は $\dfrac{2\pi}{\frac{1}{3}}=6\pi$
(3) $y=\tan 4x$ の周期は $\dfrac{\pi}{4}$
複雑な三角関数の周期
三角関数の中身(位相の部分)の $x$ の係数だけ見れば周期が分かります。それ以外の部分は周期に影響を与えません。
つまり、
$y=A\sin (kx+B)+C$ の周期は $\dfrac{2\pi}{k}$
$y=A\cos (kx+B)+C$ の周期は $\dfrac{2\pi}{k}$
$y=A\tan (kx+B)+C$ の周期は $\dfrac{\pi}{k}$
となります。$A,B,C$ は周期に関係ありません。
例題
(4) $y=\sin (3x+\pi)-1$
(5) $y=4\cos \left(\dfrac{x}{5}+\dfrac{\pi}{2}\right)$
(6) $y=0.2\tan (0.5x+0.6)+0.7$
の周期をそれぞれ求めよ。
答え
公式より、
(4) $y=\sin (3x+\pi)$ の周期は $\dfrac{2\pi}{3}$
(5) $y=4\cos \left(\dfrac{x}{5}+\dfrac{\pi}{2}\right)$ の周期は $\dfrac{2\pi}{\frac{1}{5}}=10\pi$
(6) $y=0.2\tan (0.5x+0.6)$ の周期は $\dfrac{\pi}{0.5}=2\pi$
次回は 0乗が1になることの3通りの説明 を解説します。
