1σ、2σ、3σの意味と正規分布の場合の確率

1σ、2σ、3σ区間とは

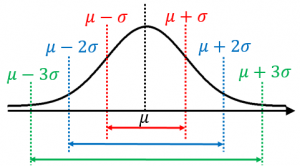
$1σ$ 区間とは、$\mu-\sigma$ から $\mu+\sigma$ までの区間です。
$2σ$ 区間とは、$\mu-2\sigma$ から $\mu+2\sigma$ までの区間です。
$3σ$ 区間とは、$\mu-3\sigma$ から $\mu+3\sigma$ までの区間です。

ただし、$\mu$ はデータ（または確率分布）の平均です：
$\mu=\dfrac{x_1+x_2+\cdots +x_n}{n}$

また、$\sigma$ はデータ（または確率分布）の標準偏差（ばらつきを表す量）です：
$\sigma=\sqrt{\dfrac{1}{n}\displaystyle\sum_{i=1}^n(x_i-\mu)^2}$
$\sigma$ はシグマと読みます。

（上の式では、データを $x_1,x_2,\cdots,x_n$ としました）

確率（正規分布の場合）

正規分布の場合、

$1σ$ 区間におさまる確率→ 約 $68.27$%
$2σ$ 区間におさまる確率→ 約 $95.45$%
$3σ$ 区間におさまる確率→ 約 $99.73$%

であることが知られています。

きちんと書くと、確率変数 $X$ が正規分布 $N(\mu,\sigma^2)$ に従うとき、
$P(\mu-\sigma\leq X\leq \mu+\sigma)\fallingdotseq 68.27$
$P(\mu-2\sigma\leq X\leq \mu+2\sigma)\fallingdotseq 95.45$
$P(\mu-3\sigma\leq X\leq \mu+3\sigma)\fallingdotseq 99.73$
というわけです。

偏差値と確率

試験の得点分布が正規分布に従うと仮定（少し強引な仮定ですが）すると、
偏差値が $40$ から $60$ の間におさまる確率が $68.27$%
偏差値が $30$ から $70$ の間におさまる確率が $95.45$%
偏差値が $20$ から $80$ の間におさまる確率が $99.73$%
と言えます。

つまり、$3$ 人に $2$ 人くらいの割合の人間が偏差値 $40$ から $60$ の間にいて、ほとんどの人間が偏差値 $20$ から $80$ の間にいると言えます。

次回は 偏差値と割合（上位何パーセントか）の変換表 を解説します。